Audit of Self

Date: January 22nd, 2025

Introduction

On January 22nd, 2025, Celo engaged zkSecurity to perform an audit of the Self project. The assessment lasted for three weeks and focused on one large monorepo as well as some provided documentation and a number of planned discussions with the team.

Scope

The original scope focused on the following three parts:

Specific core dependencies. This part of the audit focused on changes to the RSA libraries used in the project, the RSA-PSS implementation, and the ECDSA implementation (including the ECC and big-int gadgets it builds upon).
Protocol circuits and smart contracts. This part of the audit focused on the core circuits of Self used to prove the authenticity of passport data, as well as selectively disclose passport data in on-chain applications.
Proof delegation via TEEs. This part looked at the logic involved in the delegation of user proofs to AWS Nitro enclaves, AWS’s solution to a trusted execution environment (TEE).

Note that the scope was changed during the audit to redirect some of the team’s efforts on auditing the TEE code in order to focus at reviewing fixes as well.

Strategic Recommendations

We recommend the following strategic changes to the Self project:

Strengthen Testing. We recommend expanding test coverage across the protocol, particularly by incorporating more negative testing (i.e., tests designed to fail). This approach helps uncover vulnerabilities early in development. For example, the TEE Client attestation issue (see TEE Client Doesn’t Verify Enclave Attestation) could potentially have been detected through more comprehensive testing.

Enhance Code Maturity. While addressing critical issues in core dependencies (see Big Integer zero-check is not sound) is a vital step, additional measures will help ensure long-term reliability and security. We suggest devoting further engineering resources to strengthen these dependencies, particularly regarding the big integer library used for ECDSA verification (see The big integer library used for ECDSA verification is immature).

Refine the Overall Protocol. We recommend conducting a more thorough review of the protocol from an attacker’s perspective to ensure resilience against a wide range of threats. With deeper analysis, potential vulnerabilities—such as those related to second pre-image attacks (see Second pre-image attacks on PackBytesAndPoseidon may be used to register arbitrary passports and DSC certificates), signature forgery (see Trusting the start offset of the public key inside the certificate may lead to signature forgery and invalid passport registration), and enclave impersonation (see Attestation Endpoint Allows Enclave Impersonation)—could be more effectively mitigated.

Consider a Follow-Up Audit. Given the complexity of this project and the initial time constraints, we recommend scheduling a subsequent audit once the above improvements have been implemented. A deeper assessment after protocol hardening will help confirm that both the design and implementation aspects are robust and secure.

Threat model and security assumptions

All the circuits and contracts in scope have been analyzed keeping in mind some security assumptions made by the protocol, which we briefly summarize here.

Active authentication is not currently supported. While active authentication would be beneficial to the security of the protocol, it is not currently supported by Self (it is planned for a future version). Issues such as the fact that anyone that has at some point scanned the passport can register it on-chain before the real owner can, are known limitations and are not considered in scope.
Issuers are assumed to be honest. The protocol assumes that the issuers are honest, and are not compromised. The security of the protocol relies on the certificate chains emitted by the nations’ CSCAs and DSCs.
User secrets cannot be rotated or recovered. This is a limitation of the current design, which is mitigated by storing the user’s secret in the KeyChain of the mobile application. It is planned to add a recovery mechanism in the future, but currently, if the user loses their secret, they will lose access to their passport. Additionally, the phone KeyChain is trusted to be a secure storage for the user’s secret.
Accessing the passport attestation can leak if someone registered or not. The protocol computes the passport commitment deterministically from the user’s data. This means that accessing that data (e.g., with a passport scan) can leak if someone has registered that passport or not. This is a known risk, and it is not considered in scope.
Timing attacks are not in scope. The protocol can be subject to timing attacks, i.e., if a user registers a DSC certificate for its local issuer, and then immediately after registers a passport signed by that DSC, an observer can infer with a certain probability that the user is from that region. This issue is mitigated by assuming that the user will not immediately register their passport after registering the DSC certificate, which is explicitly recommended in the application, and assuming that the anonymity set is large enough to vanish possible correlations.

Methodology

All the circuits and contracts in scope have been manually reviewed. Additionally, circom-specific static analysis tools, as well as internal zkSecurity tools, have been employed to identify common flaws in the circuits.

For the cryptographic primitives we have also employed systematic testing using test vectors from the Wycheproof dataset for some selected configurations of key-length and hashing algorithms - for instance for RSA PKCS with 2048 bits and ECDSA with the p256 curve - in order to reveal subtle and common implementation errors in signature verification functions. In some cases, in order to assess the validity of a logical implementation bug, we have compared the output of the Self circom circuits against OpenSSL on the same input vectors.

Overview of Self

In this section we give a brief overview of the Self project before delving into deeper discussions.

Biometric Passport Background

passport

Biometric passports allow for two types of authentication: passive and active. All the work done by Self so far focuses on passive authentication, which is a form of authentication supported by all biometric passports.

In both cases, a passport data is indirectly signed by a Country Signing Certification Authority (CSCA) through a certificate chain that resembles the ones seen in the web public key infrastructure:

the CSCAs representing countries sign intermediary certificates called Document Signing Certificates (DSCs)
the DSCs sign passport data

In this typical public key infrastructure, root CAs (the CSCAs) are expected to be “cold” and subject to a high level of protection, while intermediary CAs (the DSCs) are expected to be “hot” (as they are continuously used in the issuance of new passports) and potentially rotated more often.

As such, verifying that a passport’s data is authentic involves verifying a certificate chain of two layers: a signature from the CSCA on an intermediary certificate, and a signature from the intermediary certificate on the passport data.

Self uses several sources to retrieve the CSCAs of different countries. Notably the ICAO, a UN entity, has a master list of root certs (CDCAs). Note in addition that different countries use different signing schemes, which are mapped on map.openpassport.app.

self map

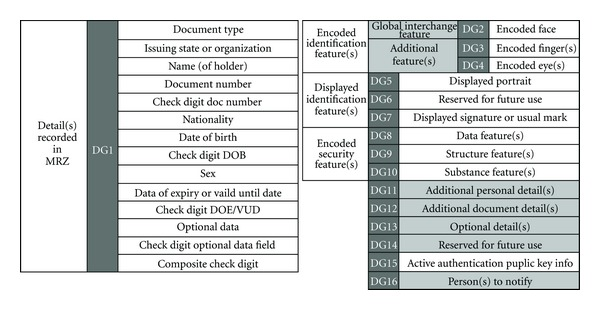
The passport data signed by a DSC is split into different data groups (DGs) where only the first two DGs are relevant in the current Self implementation:

DG1 basically has all the information you can read in the first page of a passport
DG2 is a hash of the passport picture which can nicely act as a unique identifier and can potentially help in authenticating the physical holder of the passport

All the data groups are hashed (and compressed into a Merkle tree) and then signed. From Anatomy of Biometric Passports :

data groups

Private Passport Disclosure Design

Following the explanations of the previous section, we see that to privately disclose the content of a passport we need to:

verify a CSCA signature over an intermediary certificate
verify an intermediary certificate signature over the passport data
export some specific data (e.g. full name) or prove something specific about the passport data (e.g. person is over 18)

The current Self design goes beyond that, it splits the process into three steps:

dsc: a user can prove that a DSC certificate is valid and generate a commitment to be stored in a Merkle tree (on-chain).
register: a user can register (a hiding commitment to a) passport on-chain (in a Merkle tree as well) by proving that they own a valid passport (i.e. a passport that is signed by a valid DSC)
disclose: a user can prove that there exists a registered passport, and that its content satisfies a given predicate (e.g. the person is over 18)

We go over these in more detail in a later section.

The reason for this three-step approach is that proving that signatures are valid is expensive, and one might not want to do it every time if they don’t have to. In addition, for protocols that wish to provide a “proof of person” (related to the problem of sybil resistance), Self must provide a feature that prevents passports from being used more than once.

To prevent re-registration of a passport in the first step of the flow, Self’s design has the user deterministically generate a unique identifier per-passport called a nullifier. A smart contract then stores all nullifiers seen so far, and blocks a registration attempt if its associated nullifier is already contained in the list. Hiding commitments to verified passports are then stored in a Merkle tree for easy retrieval by disclosing proofs.

Note that the commitments of valid passports stored are computed as a hash of the first two data groups, as well as some additional data. Importantly, they contain a random secret generated by the user which will become relevant later in the disclosure phase.

The smart contracts maintain three Merkle trees: one to store all the CSCA certificates supported by Self, one for all the DSCs that were proven to be part of the CSCA PKI, and one for commitments of user passports. Adding a valid intermediate certificate to the DSC certificates Merkle tree is permissionless, i.e., anyone can prove that a given certificate is valid and add it to the tree. The proof will ensure that the certificate that is added to the tree is correctly signed by a CSCA certificate that is already in the CSCA certificates Merkle tree. Subsequent registration of passport signed with a DSC certificate already in the DSC Merkle tree will use that commitment, by proving inclusion of the signer’s DCS certificate in the DSC Merkle tree.

On the other hand, a disclosing proof:

proves that a registered passport belongs in a Merkle tree previously seen before (as the Self smart contract remembers all intermediate Merkle tree roots between passport registrations)
then reconstructs the passport data from the commitment found in the Merkle tree
then proves some compliance logic (e.g. the passport is not part of an OFAC sanction)
then discloses some application-related information about the passport data (e.g. the person is over 18)
then produces a nullifier for the application

The last point, the nullifier, is simply a hash of some opaque application-specific data (e.g. the application name) and the secret used in the registration proof. This nullifier can then be stored in the application smart contract making use of Self to prevent replay attacks. Note that as a random secret is used, this nullifier is truly randomized compared to the nullifier of the registration phase, and so does not leak anything about which passport was used in the set of registered passports.

Importantly, to prevent front running a public input (unused by the circuit) is used as application-related data that is additionally authenticated by the proof. This way a proof can, for example, include the recipient of an airdrop as part of the proof, such that network observers looking to frontrun such transactions cannot extract the proof and change the recipient to themselves.

Overview of Cryptographic Primitives Implementations

Here we give an overview of the cryptographic primitives used in the Self project. The main cryptographic primitives implemented (not including hash functions) are:

RSA signature verification using PKCS1.5 padding.
RSA signature verification using PSS padding.
ECDSA signature verification.

The RSA signature verifications rely on the big integer library from zk-Email, adding padding verification on top of the existing library. The ECDSA implementation, however, relies on the circom-dl library for both elliptic curve operations and big integer emulation.

RSA signature verification

The Self project supports signature verification performed with RSA using both PKCS1.5 padding and PSS padding with multiple configurations. This is motivated by the fact that different countries support various standards and key-lengths. In the following we give a high-level overview of how these are implemented in the project. Note that, as with other signature verifications performed in this project, signatures are assumed to be performed over hashes of an original message, therefore the variables message are always assumed to be the output of a given hash function.

RSA with PKCS1.5 padding

Two similar files verifyRsa3Pkcs1v1_5.circom and verifyRsa65537Pkcs1v1_5.circom implement signature verification for RSA PCKS1.5 padding for signatures generated with public exponent $e = 3$ and $e = 65537$ respectively. They define templates i.e. template VerifyRsa65537Pkcs1v1_5(CHUNK_SIZE, CHUNK_NUMBER, HASH_SIZE) which can be instantiated with different chunk sizes, number of chunks and hash sizes, to accommodate various key sizes and hash algorithms. Concrete values for this parameters are given in a series of test circuits, for instance test_rsa_sha1_65537_2048.circom is intended to test signatures signed with a key size of 2048 bits and SHA-1 with public exponent $e = 65537$ :

template VerifyRsaPkcs1v1_5Tester() {
    signal input signature[35];
    signal input modulus[35];
    signal input message[35];

    VerifyRsa65537Pkcs1v1_5(120, 35, 160)(signature, modulus, message);
}
component main = VerifyRsaPkcs1v1_5Tester();

Both verification templates call a Pkcs1v1_5Padding template (defined in Pkcs1v1_5Padding.circom) that given a message and a modulus in input, computes the expected padded message. This is then compared to the output of the operation $s^{e} m o d n$ for a given signature $s$ .

RSA with PSS padding

For this padding also two templates handle the public exponents $e = 3$ and $e = 65537$ respectively, namely rsapss3.circom and rsapss65537.circom. They both rely on the mask generation template mfg1.circom that implements a mask as described in the PSS specification. Test show examples of concrete parameters passed to the templates to handle various key lengths, hashing functions and salt lengths, for instance:

template VerifyRsaPss3Sig_tester() {
    signal input modulus[35];
    signal input signature[35];
    signal input message[256];

    VerifyRsaPss3Sig(120, 35, 32, 256, 2048)(modulus,signature,message);
}

component main = VerifyRsaPss3Sig_tester();

instantiates the case of 2048-bit public key length, used in combination with SHA-256 and 32 bit salt length for $e = 3$ . Note that different from RSA PKCS1 the input message is not an array of chunks but an array of bits.

Big integers

Big integers used for ECDSA verification are implemented in the utils/crypto/bigInt directory. An integer is represented as an array of field elements, called chunks. This representation is parametrized by two constants:

CHUNK_SIZE: The bit length of the values in each chunk.
CHUNK_NUMBER: The number of chunks used to represent the integer.

For example, a 512-bit integer can be represented using 8 chunks of 64 bits each, corresponding to CHUNK_SIZE = 64 and CHUNK_NUMBER = 8.
From now on, we denote CHUNK_NUMBER as $n$ and CHUNK_SIZE as $k$ .

Given chunks $c_{i}$ , the underlying integer is computed as:

N = \sum_{i = 0}^{n} 2^{k \cdot i} \cdot c_{i}

An integer is considered overflow-free if every chunk $c_{i}$ is in the range $[0, 2^{k})$ . In this case, every $n \cdot k$ -bit integer has a unique representation.

The library provides an implementation of operations on big integers, enabling arithmetic operations, comparisons, and foreign field emulation. To optimize arithmetic operations, the library offers several overflow templates (indicated by overflow in their names). These perform arithmetic operations without normalizing the chunks at the end. For example:

BigAddOverflow: Computes the element-wise sum of the chunks.
ScalarMultOverflow: Multiplies each chunk by a scalar value, without normalizing the result.

For overflow multiplication, the library provides two implementations:

Standard element-wise multiplication using the limbs.
Karatsuba algorithm, which is more efficient for specific parameter choices.

The decision of which algorithm to use is made at circuit-generation time using is_karatsuba_optimal_dl().

To assert that an integer $N$ is zero modulo some number $m$ , the prover witnesses the quotient $q$ and the remainder $r$ of the division $N / m$ . The circuit then asserts that:

q \cdot m - N

is the big integer corresponding to zero, using BigIntIsZero.

Another example is the BigMultModP template, which computes the product of two big integers $x$ and $y$ , reduced modulo some integer $m$ .

Compute $x \cdot y$ using BigMultOverflow.
The prover witnesses a quotient $q$ and remainder $r$ for $x \cdot y \div m$ .
The circuit asserts that:
$q \cdot m + r - x \cdot y$

is the big integer corresponding to zero, using BigIntIsZero.

Elliptic curve operations

Elliptic curve operations are implemented in the utils/crypto/ec directory, and are part of the circom-dl library. They make use of the big integer library for arithmetic operations on the base field of the curve. Recall that an elliptic curve is defined as the set of points $(x, y)$ that satisfy the curve equation

y^{2} = x^{3} + a x + b

over some base field $𝔽_{p}$ , where $a$ and $b$ and $p$ are the curve parameters.

There are three main templates that implement useful assertions over elliptic curve points.

PointOnCurve checks if a point $(x, y)$ lies on the curve, i.e., it checks that the curve equation holds over the base field of the curve. It does so by computing the following quantity

Z = y^{2} - (x^{3} + a * x + b)

and then asserts that $Z = 0 \mod p$ using BigIntIsZeroModP.

PointOnTangent checks if a point $(x_{1}, - y_{1})$ lies on the tangent of the curve at a given point $(x_{0}, y_{0})$ . Since this template is used in point doubling, the y coordinate of the checked point is negated. First, the slope of the tangent line to the point $(x_{0}, y_{0})$ is computed as

λ = \frac{3 \cdot x_{0}^{2} + a}{2 \cdot y_{0}}

Then, the tangent line is evaluated at the x coordinate $x_{1}$ to get the corresponding y coordinate $y_{1}$ .

\bar{y_{1}} = λ \cdot (x_{1} - x_{0}) - y_{0}

The check should pass if $y_{1} = \bar{y_{1}}$ . Simplifying the equation, we need to assert that

2 \cdot y_{0} \cdot (y_{1} + y_{0}) = (3 \cdot x_{0}^{2} + a) \cdot (x_{1} - x_{0})

holds over the base field, which is again implemented using BigIntIsZeroModP.

Lastly, PointOnLine checks if three points $(x_{1}, y_{1})$ , $(x_{2}, y_{2})$ , and $(x_{3}, - y_{3})$ are collinear. Since this template is used in point addition, the y coordinate of the third point is negated. Co-linearity is checked by asserting that the following relation

(y_{1} + y_{3}) \cdot (x_{2} - x_{1}) = (y_{2} - y_{1}) \cdot (x_{1} - x_{3})

holds over the base field, again using BigIntIsZeroModP.

To compute the sum of two points $P = (x_{1}, y_{1})$ and $Q = (x_{2}, y_{2})$ , the following steps are performed: - the result is witnessed $R = (x_{3}, y_{3})$ - the circuit asserts that $(x_{3}, y_{3})$ is a point on the curve using PointOnCurve. - the circuit asserts co-linearity of $P$ , $Q$ , and $- R$ using PointOnLine.

To compute the doubling of a point $P = (x_{1}, y_{1})$ , the following steps are performed: - the result is witnessed $R = (x_{2}, y_{2})$ - the circuit asserts that $(x_{2}, y_{2})$ is a point on the curve using PointOnCurve - the circuit asserts that the point $R$ lies on the tangent line of the curve at $P$ using PointOnTangent.

Scalar multiplication is performed using an optimized windowed approach, where the scalar is split into chunks of bits, also known as the Pippenger algorithm. For scalar multiplication with the base point $G$ , it is used instead a more efficient template, that makes use of precomputed powers of the generator. The precomputed values are stored in the ec/powers directory, and are given for multiple standard curves.

ECDSA verification

Self supports signature verification performed with ECDSA with multiple configuration of hashes and curves. The following curves are supported: - brainpoolP224r1 - brainpoolP256r1 - brainpoolP384r1 - brainpoolP512r1 - p256 - p384 - p521

Signature verification assumes that signatures are generated over the hash of the original message, with an additional preprocessing step applied to the hash based on the following conditions: - Truncation: If the hash length exceeds or equals the scalar field size in bits, the rightmost bits are truncated. - Padding: If the hash length is shorter than the scalar field size, leading zeroes are added (left-padding) to match the required bit length.

The ECDSA signature verification accept the following inputs: - signature: Signature component $(r, s)$ , where each element is represented in bigint. - pubkey: Public key used for verify the signature, consist of elliptic curve point $(x, y)$ represented in bigint. - hashed: The hash of the message to be verified, represented as array of bits.

Below is a structured overview of the verification flow:

The value of hashed is transformed to the bigint representation by grouping into $k$ bits of chunk, where $k$ is chunk number that set in the template parameter, and convert each chunk to the numeric form using Bits2Num template. These chunks are stored in hashedChunked.
Retrieve the order of the elliptic curve $n$ using EllipicCurveGetOrder function.
Compute modular inverse of $s$ (denoted $s^{- 1} \mod n$ ) using BigModInv template.
Compute $u_{1} = s^{- 1} \cdot h \mod n$ and $u_{2} = s^{- 1} \cdot r \mod n$ using modular multiplication BigMultModP, where $h$ is the value of hashedChunked.
Compute $u_{1} \cdot G$ using EllipticCurveScalarGeneratorMult, where $G$ is the curve’s base point.
Compute $u_{2} \cdot p u b k e y$ using EllipticCurveScalarMult.
The previous two computed points are added together (ie. $u_{1} \cdot G + u_{2} \cdot p u b k e y$ ) using EllipticCurveAdd, resulting in $(x 1, y 1)$ .
Verify that $x 1 = r$ by comparing the equality of each chunks.

Overview of the Main Protocol Circuits

There are three main circuits that are used in the protocol:

The DSC circuit verifies the signature of a DSC certificate using a CSCA certificate in the CSCA tree, and additionally generates a leaf to be appended in the DSC tree.
The registration circuit verifies the signature of a passport using a DSC certificate in the DSC tree, and additionally generates a commitment to be stored on-chain, and a nullifier to prevent double registration of the same passport.
The disclose circuit allows to disclose some selected information about the passport data, and generates a nullifier that can be application-specific.

DSC circuit

The purpose of the DSC circuit is to verify that a DSC certificate is signed by one of the CSCA certificates in the CSCA tree, and to generate a leaf to be appended in the DSC tree. First, it takes in input the raw CSCA bytes, and a Merkle proof of the inclusion in the CSCA tree. The bytes are packed and hashed to generate the leaf, and the Merkle root is computed using the Merkle proof. The computed Merkle root is constrained to be equal to the root which is passed as a public parameter by the verification contract.

Additionally, the public key of the CSCA is passed in input represented as an array of chunks. This additional input is verified to be consistent with one sequence of bytes in the original CSCA certificate, which is done by comparing it with a subarray of the CSCA certificate with bounds provided by the prover. The bounds are checked to be consistent with the size of the public keys of the specific algorithm parameters used.

Finally, the hash digest of the raw DSC certificate is computed, and the signature is verified using the public key of the CSCA. A commitment to the DSC certificate is also generated, computed as

dsc_leaf = Poseidon(Poseidon(Poseidon(raw_dsc), raw_dsc_len), csca_tree_leaf)

which is given in output by the circuit, and is inserted in the DSC tree.

Registration circuit

The purpose of the registration circuit is to verify that a passport data is correctly signed by a DSC certificate in the DSC tree, and to generate a commitment to the passport and a nullifier to prevent double registration of the same passport. As before, the raw DSC certificate is given in input, and its hashed is checked for inclusion in the DSC Merkle tree. The public key of the DSC certificate is also passed in input, and is verified to be consistent with the DSC certificate bytes, by comparing it with a subarray of the DSC certificate with bounds provided by the prover. As for te DSC circuit, the bounds are checked to be consistent with the size of the public keys of the specific algorithm parameters used.

The passport data and the signature are verified using the PassportVerifier template, which hashes the sections of the passport data and verifies the signature to be valid using the public key extracted from the DSC certificate. Finally, a passport commitment is computed as

passport_leaf = Poseidon(secret, 1, Poseidon(dg1), Poseidon(eContent_hash), dsc_tree_leaf)

Additionally, the nullifier is computed as the poseidon output of the sha hash of the signed attributes. Both the commitment and the nullifier are given in output by the circuit and stored on-chain.

Disclose circuit

The purpose of the disclose circuit is to verify that some disclosed information about a passport are consistent with the previously verified passport data. To do so, the circuit verifies that the prover knows some data and a secret key such that the computed commitment is in the passports Merkle tree. After verifying the commitment, it checks that the disclosed data are consistent with the passport data. The prover can select which data or property about the passport to disclose using selector inputs. Finally, the circuit generates a nullifier, which is computed together with a “scope”, which could be the name of the app or event that we are disclosing our information to. The nullifier is simply a poseidon of the user’s secret and the scope, and it is used to ensure that the same user can perform only one disclosure for each scope.

Overview of the Self Smart Contracts

The Self contracts consist of three main components that handle different aspects of passport verification and identity management.

The IdentityVerificationHub manages all interactions between users’ zero-knowledge proofs and the on-chain identity registry. It maintains mappings to multiple verifier contracts to handle different types of proof circuits. When users submit proofs, the hub routes them to the appropriate verifier contract and, upon successful verification, triggers the IdentityRegistry to record the user’s commitment.

The IdentityRegistry contract is the on-chain ledger for user identity commitments. It implements a Lean Incremental Merkle Tree to efficiently store and prove the existence of identity commitments. Each commitment in the tree corresponds to a verified passport, and the registry maintains a mapping of nullifiers to prevent double registration of the same passport. The registry also stores and manages two important Merkle roots: - The OFAC root to enforce sanctions checks - The CSCA root to verify the authenticity of DSC certificates

Every time a commitment is added, removed, or updated, the registry generates and timestamps a new Merkle root to create an auditable history of the system’s state.

The PassportAirdropRoot contract demonstrates how applications can build on top of this infrastructure. It verifies that users possess valid passports through Verify Commitment (VC) and Disclose proofs. These proofs are verified against predetermined parameters such as - a specific scope (a unique identifier for the application), - an attestation identifier (a unique identifier for the type of attestation, e.g., an e-passport attestation), - and — optionally — a root timestamp from the identity registry.

The PassportAirdropRoot contract implements its own nullifier tracking to prevent that users can register their address for the airdrop twice. Thus, it provides an instructive example of how applications can maintain their own state while leveraging Self’s core verification infrastructure.

To allow for future improvements while maintaining stable contract addresses and state, Self’s smart contracts make use of the Universal Upgradeable Proxy Standard (UUPS). Access between contracts is strictly controlled, with the IdentityRegistry only accepting commitment registrations from the IdentityVerificationHub, and administrative functions being restricted to an authorized contract-owner address.

IdentityVerificationHub

The IdentityVerificationHub contract serves as the central verification point for all zero-knowledge proofs in the system. It manages verifier mappings to handle different types of proofs and coordinates with the IdentityRegistry for commitment storage.

The contract maintains two primary verifier mappings: - sigTypeToRegisterCircuitVerifiers: Maps signature types to their corresponding register circuit verifiers - sigTypeToDscCircuitVerifiers: Maps signature types to their corresponding DSC circuit verifiers

These mappings enable the hub to route proofs to the appropriate external verifier contracts based on the signature type being verified. When a user submits a proof, the hub: 1. Identifies the correct verifier contract from its mappings 2. Calls the verifier with the proof and public inputs 3. Upon successful verification, instructs the IdentityRegistry to store the user’s commitment

For VC and Disclose proofs, the hub uses a dedicated vcAndDiscloseCircuitVerifier to verify inclusion proofs. These proofs demonstrate that a previously registered passport commitment exists in the IdentityRegistry’s Merkle tree and satisfies specific predicates.

The hub also provides utility functions to convert the output of vcAndDisclose circuits into a readable format, which allows external contracts to access and verify specific passport attributes.

IdentityRegistry

The IdentityRegistry contract is the on-chain storage layer for identity commitments, and maintains several important data structures:

An Incremental Merkle Tree of identity commitments
A mapping of nullifiers to prevent double registration
A mapping of root timestamps
External Merkle roots: ofacRoot and cscaRoot

When the IdentityVerificationHub verifies a proof successfully, it calls the registry’s registerCommitment function to store the new commitment in the Merkle tree. Before insertion, the contract checks that the associated nullifier hasn’t been used before, preventing the same passport from being registered multiple times.

Each time the Merkle tree is modified through commitment registration, the contract generates a new root and records its timestamp. This creates a historical record of valid roots, which is necessary for proving inclusion at specific points in time. External contracts can verify these timestamps using the rootTimestamps mapping.

The registry also maintains two external Merkle roots that are important for the verification process: - ofacRoot: Used for sanctions compliance checks - cscaRoot: Used to verify the authenticity of DSC certificates in passports

In addition, the contract includes several “development functions” (prefixed with dev) to provide the contract owner with certain admin capabilities for testing, maintenance, and emergency interventions:

devAddIdentityCommitment: Forces the addition of an identity commitment without proof verification
devUpdateCommitment: Updates an existing commitment in the Merkle tree
devRemoveCommitment: Removes a commitment from the Merkle tree
devAddDscKeyCommitment: Forces the addition of a DSC key commitment
devUpdateDscKeyCommitment: Updates an existing DSC key commitment
devRemoveDscKeyCommitment: Removes an existing DSC key commitment
devChangeNullifierState: Directly modifies the state of a nullifier
devChangeDscKeyCommitmentState: Directly modifies the registration state of a DSC key commitment

Many of the registry’s functions come with strict access control. Only the IdentityVerificationHub can register new commitments, and only the contract owner can update the OFAC/CSCA roots or call the above-mentioned dev functions.

As a summary, the registry represents the system’s storage layer, focusing exclusively on identity-commitment storage and Merkle root management while delegating all proof verification logic to the IdentityVerificationHub.

PassportAirdropRoot

The PassportAirdropRoot contract demonstrates a practical implementation of the Self system. More specifically, it provides a reference implementation for token airdrops based on passport verification, and shows how to securely register users for an airdrop while ensuring each passport can only be used once to claim tokens.

For each airdrop claim attempt, the contract performs the following steps: 1. Verifies the VC and Disclose proof using the IdentityVerificationHub 2. Validates that the proof’s scope matches the expected value (e.g., “airdrop-v1”) 3. Confirms the attestation identifier matches the expected value (typically “1” for e-passports) 4. Checks that the nullifier (derived from the passport and airdrop scope) hasn’t been used before 5. If a snapshot timestamp is specified, verifies that the Merkle root used in the proof existed in the IdentityRegistry at that time 6. Records the nullifier to prevent double-claiming of the airdrop with the same passport 7. Emits a UserIdentifierRegistered event containing the user’s identifier for the airdrop distribution

Thus, the contract provides an instructive example of how projects can build on top of the core Self infrastructure while maintaining their own application-specific state and verification requirements.

Proof Delegation Using TEEs

Due to the high number of constraints of its circuits, Self has users delegate their zero-knowledge proof generation to Trusted Execution Environments (TEEs). This way, even small constrained user devices can make use of the Self service. This section describes what TEEs are, and how the proof delegation protocol works.

Trusted Execution With AWS Nitro Enclaves

A Trusted Execution Environment (TEE) is a secure, isolated area of a processor that guarantees integrity for the code it runs and confidentiality for the data it handles. This isolation means even the host operating system cannot see or tamper with the TEE’s internal state.

AWS Nitro Enclaves offer TEEs on Amazon EC2 instances by providing:

Dedicated vCPUs and Memory: An enclave is allocated specific hardware resources, separated from the host OS.
Nitro Secure Module (NSM): A hardware component that provides secure randomness, cryptographic operations, and remote attestation capabilities.
Minimal Attack Surface: Since the only way for the host to communicate with its enclave is via a vsock, potential attack vectors are greatly reduced.

In essence, Nitro Enclaves allow users to offload sensitive tasks, such as key management, zero-knowledge proof generation, and cryptographic attestations—into an isolated environment.

Other applications can trust the Nitro enclave’s output thanks to its attestations. Attestations are cryptographically signed documents, generated in this case by the Nitro Secure Module (NSM), that proves:

TEE Integrity: The measurement (hash) of the enclave’s file system, including the application code, matches an expected version.
Session Binding: It embeds contextual data—such as ephemeral public keys, nonces, and user data to ensure the session is unique and not replayed.

Attestations are signed as part of AWS public-key’s infrastructure, where the Nitro secure module public key is itself signed by other AWS keys, eventually signed by one of AWS root keys, forming what is called a certificate chain.

By verifying an attestation and its certificate chain, a client knows it is communicating with a genuine TEE running the intended code. As such, it can, for example, encrypt its user data to the enclave without exposing them to anyone else, including the cloud operators.

High-Level Proof Delegation Flow

Self’s TEE service produces zero-knowledge proofs on behalf of clients. Clients rely on the enclave to compute proofs while keeping the inputs private. The protocol is implemented in the following high-level steps:

Both the user and the enclave perform an ephemeral ECDH key exchange to establish an encrypted channel for subsequent requests.
Proof generations are queued up, and clients must check the result asynchronously.

TEE server initialization. When the TEE server (enclave) starts:

It initializes the communication channel with the NSM device, giving it access to randomness and attestation services.
Launches an RPC server to handle incoming requests from the client (proxied through the host).
Connects to a database to record proof-generation requests and statuses (proxied through the host).

Self runs three Nitro Enclave instances—one per circuit type: register, dsc, and disclose.

Hello endpoint. Once the client wants to generate a proof, it requests a new session with the enclave by hitting a “hello” RPC endpoint (run within the enclave). The endpoint performs the following steps:

parses the client request as (uuid, U) where uuid is a unique request ID and U is the client’s public key
the server produces an ephemeral keypair
the server produces an attestation on the user’s public key and the ephemeral keypair
the server performs a key exchange using both keys, derives the shared secret, and stores it along with the uuid in memory
the server returns the attestation

Request endpoint. Once this session is established, the client can send a unique proof generation (as each proof generation is associated with a unique uuid) by hitting the request endpoint. The endpoint performs the following steps:

parses the client request as (uuid, C, onchain) where C is the encrypted request body (containing an IV/nonce, a ciphertext, and an authentication tag for AES-GCM), and onchain determines if the proof is eventually submitted to a Celo smart contract or some backend SDK
retrieves the shared secret associated with the uuid and decrypts the ciphertext
parses the circuit name from the encrypted request (i.e. register, dsc, or disclose)
inserts a record into the database (tying it to uuid) and triggers the async proof-generation pipeline.
returns the uuid to the client indicating the request was accepted

The client can then use uuid to track the status of the proof generation.

Async proof-generation process. Once the TEE accepts a request, which includes the inputs necessary for generating proof and the proof type, it runs a pipeline to produce the requested zero-knowledge proof in the background. This process has three stages:

Store User Inputs. Saves both private and public inputs to inputs.json in a temporary folder named tmp_uuid. Update the request status to Pending in DB.
Generate Witnesses. Use the circuit-specific witness generator (e.g., in a folder matching the circuit name) to produce output.wtns. Update the request status to WitnessesGenerated in DB.
Generate Proof. Invoke rapidsnark to generate the final proof (proof.json) from output.wtns. Also record public inputs/outputs in public_inputs.json. Update the request status to ProofGenerated, while saving both the public inputs and the generated proof in DB.

If any error occurs, the temporary folder is removed. Similarly, after successful proof generation, the tmp_uuid folder is deleted to save disk space. However, there is currently no recovery mechanism if the TEE server restarts mid-pipeline; the request must then be resubmitted under a new uuid.

Proof relayer. A separate service, called a Proof Relayer, monitors the database for newly generated proofs. It then submits these proofs to the designated endpoint: either the Celo Network (on-chain transaction) or a Backend SDK (an off-chain service or API).

By offloading submission to a relayer, the client does not need to remain connected or manually retrieve and send the proof by themselves.

Findings

Below are listed the findings found during the engagement. High severity findings can be seen as so-called "priority 0" issues that need fixing (potentially urgently). Medium severity findings are most often serious findings that have less impact (or are harder to exploit) than high-severity findings. Low severity findings are most often exploitable in contrived scenarios, if at all, but still warrant reflection. Findings marked as informational are general comments that did not fit any of the other criteria.

ID	Component	Name	Risk
#00	TEE client	TEE Client Doesn't Verify Enclave Attestation	High
#01	TEE server	Attestation Endpoint Allows Enclave Impersonation	High
#02	dependencies circuits	Big Integer Zero-Check Is Not Sound	High
#03	protocol circuits	Exclusion Check Of Forbidden Countries Is Unsound And Incomplete Due To Incorrect Indexing	High
#04	protocol circuits	Second Pre-Image Attacks On PackBytesAndPoseidon May Be Used To Register Arbitrary Passports And DSC Certificates	High
#05	protocol circuits	Trusting The Start Offset Of The Public Key Inside The Certificate May Lead To Signature Forgery And Invalid Passport Registration	High
#06	TEE client	Harden TEE Client and Server Communication	Medium
#07	TEE server	TEE Server Memory Grows Unbounded	Medium
#08	dependencies circuits	The Big Integer Library Used For Ecdsa Verification Is Immature	Medium
#0a	protocol circuits	Off-By-One In Dsc Padding Check	Medium
#0b	TEE server	Potential DoS Vector In TEE Server Hello Endpoint	Low
#0c	dependencies circuits	Missing Range Check On The Chunk Sizes In ECDSA	Low
#0d	dependencies circuits	Missing Range Check In The Ecdsa Signature Component	Low
#0e	dependencies circuits	Over-Constraint In Ecdsa For Large x1 Coordinate	Low
#0f	dependencies circuits	Over-Constraint In Ecdsa For Point Duplication	Low
#10	dependencies circuits	Over-Constraint In ECDSA For Edge Case In Scalar Multiplication	Low
#11	dependencies circuits	Missing Range Check On The Chunk Sizes In RSA-PSS	Low
#12	dependencies circuits	Missing Constraint On The Padding In RSA-PSS	Low
#13	dependencies circuits	Missing Range Check On The Signature In RSA-PSS	Low
#14	dependencies circuits	Multiple Missing Constraints On The Padding In RSA-PSS	Low
#15	protocol circuits	Wrong Ceil Division in Message Chunk Computation	Low
#16	TEE client	Consider Making TEE Attestations More Auditable	Informational
#17	contracts	Smart Contracts Are Not Following Some Solidity Coding Standards	Informational

#00 - TEE Client Doesn't Verify Enclave Attestation

Severity: High Location: TEE client

Description. When delegating the creation of proofs to a TEE, the client must verify that the TEE’s public key is legitimate before using it to encrypt its witness.

This is done in app/src/utils/proving/attest.ts by verifying a certificate chain with a hardcoded root AWS certificate:

/**
 * @notice Verifies a certificate chain against a provided trusted root certificate.
 * @param rootPem The trusted root certificate in PEM format.
 * @param certChainStr An array of certificates in PEM format, ordered from leaf to root.
 * @return True if the certificate chain is valid, false otherwise.
 */
export const verifyCertChain = (
  rootPem: string,
  certChainStr: string[],
): boolean => {
  try {
    // Parse all certificates
    const rootCert = new X509Certificate(rootPem);
    const certChain = certChainStr.map(cert => new X509Certificate(cert));

    // Verify the chain from leaf to root
    for (let i = 0; i < certChain.length; i++) {
      // TRUNCATED...

      // Verify signature
      try {
        const isValid = currentCert.verify(issuerCert);
        if (!isValid) {
          console.error(<!--CODE_BLOCK_1203-->);
          return false;
        }
      } catch (e) {
        console.error(<!--CODE_BLOCK_1204-->, e);
        return false;
      }
    }
    console.log('Certificate chain verified');
    return true;

The previous code is insecure as it never returns false on invalid signatures. This is because the call to verify returns a Promise<boolean> which is always set, and thus always passes the test if (!isValid) on the next line.

Reproduction steps. You can reproduce the following bug by passing a bogus certificate chain to the verifyCertChain function:

'use strict';

const { verifyCertChain } = require('./attest');
const { AWS_ROOT_PEM } = require('./awsRootPem');

const ZKSECURITY_CERT = `-----BEGIN CERTIFICATE-----
MIIDTjCCAjYCCQDklcss2TB/STANBgkqhkiG9w0BAQsFADBpMQswCQYDVQQGEwJV
UzETMBEGA1UECAwKQ2FsaWZvcm5pYTEWMBQGA1UEBwwNU2FuIEZyYW5jaXNjbzEU
MBIGA1UECgwLRXhhbXBsZSBJbmMxFzAVBgNVBAMMDnprc2VjdXJpdHkueHl6MB4X
DTI1MDIxMjAyMjUwMloXDTI2MDIxMjAyMjUwMlowaTELMAkGA1UEBhMCVVMxEzAR
BgNVBAgMCkNhbGlmb3JuaWExFjAUBgNVBAcMDVNhbiBGcmFuY2lzY28xFDASBgNV
BAoMC0V4YW1wbGUgSW5jMRcwFQYDVQQDDA56a3NlY3VyaXR5Lnh5ejCCASIwDQYJ
KoZIhvcNAQEBBQADggEPADCCAQoCggEBANgawMtkBuxW5IGfdunO48fVz3n5GEdS
YI78Mgc9LZaGUApBa8LxHOmPlSoNbdCpiZvR0R8MND3J/11nJZtL6WRMU6fBKrwJ
0X96TIC6Wh58ut9KvjMMmvbrnNFTDrpKEac33Mbwiqul4OF7EhZZtOCacOtv0STW
m0ZZn4o4YUNRgvoa71TjmkRfFbOl+K1biMzkAnCwVXVhBFdbzbRdfIlXTTeElhF6
jtty01WLNsSanjdD1TqVlaN0mEPx6lFOU+O4ZyPMrmulpE/9xP2u4f7rbS+i3qIa
pdF4X5pCXmCewC04b+oo1vKTCzPXPqrS2EvwKWySgZyiUWuSfKHoULsCAwEAATAN
BgkqhkiG9w0BAQsFAAOCAQEAX+S49/xcUCO9pN5GX/+4xofdpWVkc+LQY8JpnBm5
FlUTKcBSDxfQupDqjljtsQxnx99ZtE+O1+3imbON1G/CyPLPnr2w6UhVZa5Xq+M7
By7bwikDBwk/LilD+UKn1B98oh3xRTPeH6u351JLDTOc1hwLd01DKBpSwdkgR5Kj
lZJQUAzJP/0cg0158vtxV2Y9ob2yyrYk6kYIKEo3WtP1uQyAU4l8Gv00f3LtjjTk
egozp5+TRbiPhEr6AkakvWgR6yDLfMLwn+iib/BhQ4CMlC6FPeYUP24qrwXZaL2B
L0bX5MgLY4ouiknAvYbfgE0Wx/pyb6xq7h1COm/uevhceg==
-----END CERTIFICATE-----`;

const invalidChain = [ZKSECURITY_CERT];
const invalidChainResult = verifyCertChain(AWS_ROOT_PEM, invalidChain);
console.log('verifyCertChain(invalidChain) result:', invalidChainResult);

Recommendation. Ensure that the verify function is properly awaited before checking its result.

Client Response. The update replaces X509Certificate.verify() with a custom ECDSA (p384/sha384) verification function and reorders the certificate chain so the first entry is the root. Since this custom verification is synchronous, the result can be checked without await. However, the verifyCertChain function returns a Promise unnecessarily after these changes.

#01 - Attestation Endpoint Allows Enclave Impersonation

Severity: High Location: TEE server

Description. The attestation endpoint of the service deployed in the Nitro enclave allows a user to request Nitro enclave attestations with arbitrary public_key, user_data, and nonce fields.

You can see that in tee-prover-server/src/server.rs:

async fn attestation(
        &self,
        user_data: Option<Vec<u8>>,
        nonce: Option<Vec<u8>>,
        public_key: Option<Vec<u8>>,
    ) -> ResponsePayload<'static, Vec<u8>> {
        let request = Request::Attestation {
            user_data: user_data.map(|buf| ByteBuf::from(buf)),
            nonce: nonce.map(|buf| ByteBuf::from(buf)),
            public_key: public_key.map(|buf| ByteBuf::from(buf)),
        };

        let result = match nsm_process_request(self.fd, request) {
            Response::Attestation { document } => ResponsePayload::success(document),
            // TRUNCATED...
        };

        return result;
    }

This is insecure as this allows anyone to forge enclave attestations for their own public key, instead of the Nitro enclave public key.

This violates the TEE claimed properties, allowing Self, cloud operators, or malicious users with a privileged network position to impersonate the enclave and leak user data. This is possible as the flow of the protocol from the user’s perspective is to encrypt their witness data with the public key contained in the attestation.

Recommendation. We recommend removing the attestation endpoint which does not seem to serve any purpose in the protocol’s flow.

Client Response. The update excludes the user_data and public_key, but the attestation endpoint still exists.

#02 - Big Integer Zero-Check Is Not Sound

Severity: High Location: dependencies circuits

Description. One of the core operation that is used throughout the big integer implementation is the assertion for a zero element. It is implemented in the template BigIntIsZero and is used in multiple places in the library.

template BigIntIsZero(CHUNK_SIZE, MAX_CHUNK_SIZE, CHUNK_NUMBER) {
    assert(CHUNK_NUMBER >= 2);

    var EPSILON = 3;

    assert(MAX_CHUNK_SIZE + EPSILON <= 253);

    signal input in[CHUNK_NUMBER];

    signal carry[CHUNK_NUMBER];
    for (var i = 0; i < CHUNK_NUMBER - 1; i++){
        if (i == 0){
            carry[i] <== in[i] / 2 ** CHUNK_SIZE;
        }
        else {
            carry[i] <== (in[i] + carry[i - 1]) / 2 ** CHUNK_SIZE;
        }
    }
    component carryRangeCheck = Num2Bits(MAX_CHUNK_SIZE + EPSILON - CHUNK_SIZE);
    carryRangeCheck.in <== carry[CHUNK_NUMBER - 2] + (1 << (MAX_CHUNK_SIZE + EPSILON - CHUNK_SIZE - 1));
    in[CHUNK_NUMBER - 1] + carry[CHUNK_NUMBER - 2] === 0;
}

This component checks the following relation:

\sum_{i = 0}^{CHUNK\_NUM} C_{i} \cdot 2^{CHUNK\_SIZE \cdot i} = 0

It does so by first accumulating the carries, then range checking the final carry value and then asserting that the final carry is the opposite of the most significant chunk. However, the accumulation of the carries is performed over the native field, so the entire relation is checked modulo the Circom native prime.

This bug does not compromise completeness, as the zero integer will still be considered as zero modulo the native prime. However, this check is not sound, as a non-zero integer, which is zero mod native prime, will be considered zero by the library.

Impact. To show impact, we provide a valid input for the PointOnCurve template, instantiated on the BrainpoolP512R1 curve, which satisfies the constraints but is not a valid point on the curve. To assert that a point $(x, y)$ lies on a curve, the circuits computes

Z = y^{2} - x^{3} + a \cdot x + b

and then it asserts that $Z = 0 \mod p$ using BigIntIsZeroModP, which internally uses BigIntIsZero. To make this check pass with an invalid point, it suffices to find a pair of coordinates that satisfy the curve equation modulo the Circom prime, but not modulo the curve prime.

from sage.all import GF, EllipticCurve
import json

circom_p = 21888242871839275222246405745257275088548364400416034343698204186575808495617

# we want to represent 512 bit numbers, 8 chunks of 64 bits
CHUNK_SIZE = 64
CHUNK_NUMBER = 8


def split_into_chunks(p, chunk_size):
    chunks = []
    for i in range(chunk_size):
        chunks.append((p >> (i * CHUNK_SIZE)) % (2 ** CHUNK_SIZE))
    return chunks


def int_from_chunks(chunks):
    p = 0
    for i, chunk in enumerate(chunks):
        p += chunk * (2 ** (i * CHUNK_SIZE))
    return p

brainpool_p = 0xaadd9db8dbe9c48b3fd4e6ae33c9fc07cb308db3b3c9d20ed6639cca703308717d4d9b009bc66842aecda12ae6a380e62881ff2f2d82c68528aa6056583a48f3
brainpool_a = 0x7830a3318b603b89e2327145ac234cc594cbdd8d3df91610a83441caea9863bc2ded5d5aa8253aa10a2ef1c98b9ac8b57f1117a72bf2c7b9e7c1ac4d77fc94ca
brainpool_b = 0x3df91610a83441caea9863bc2ded5d5aa8253aa10a2ef1c98b9ac8b57f1117a72bf2c7b9e7c1ac4d77fc94cadc083e67984050b75ebae5dd2809bd638016f723
BrainpoolP512R1 = EllipticCurve(GF(brainpool_p), [brainpool_a, brainpool_b])

def sqrt_mod_circom_p(x):
    return int(GF(circom_p)(x).sqrt())

# we take x = circom_p + 1, and compute y accordingly over GF(circom_p)
x_forged = circom_p + 1
y_forged = sqrt_mod_circom_p(brainpool_b + brainpool_a + 1)

assert is_on_curve_circuit(x_forged, y_forged)

# the coordinates satisfy the curve equation over the native field
assert (y_forged * y_forged) % circom_p == (x_forged * x_forged * x_forged + brainpool_a * x_forged + brainpool_b) % circom_p

# however, the point is not in the curve
assert (y_forged * y_forged) % brainpool_p != (x_forged * x_forged * x_forged + brainpool_a * x_forged + brainpool_b) % brainpool_p
assert BrainpoolP512R1.lift_x(GF(brainpool_p)(x_forged), all=True) == []

with open("input.json", "w") as f:
    json.dump({
        "in": [
            list(map(str, split_into_chunks(x_forged, CHUNK_NUMBER))),
            list(map(str, split_into_chunks(y_forged, CHUNK_NUMBER)))
    ]}, f)

We can then instantiate a circuit for the PointOnCurve template using the BrainpoolP512R1 curve parameters.

include "../utils/crypto/ec/curve.circom";

// template PointOnCurve(CHUNK_SIZE, CHUNK_NUMBER, A, B, P)
component main = PointOnCurve(64, 8,
    [
        16699818341992010954,
        9156125524185237433,
        733789637240866997,
        3309403945136634529,
        12120384836935902140,
        10721906936585459216,
        16299214545461923013,
        8660601516620528521
    ],
    [
        2885045271355914019,
        10970857440773072349,
        8645948983640342119,
        3166813089265986637,
        10059573399531886503,
        12116154835845181897,
        16904370861210688858,
        4465624766311842250
    ],
    [
        2930260431521597683,
        2918894611604883077,
        12595900938455318758,
        9029043254863489090,
        15448363540090652785,
        14641358191536493070,
        4599554755319692295,
        12312170373589877899
    ]
);

It suffices then to change the witness generation of div_result in BigIntIsZeroModP and the circuit will accept the forged point as a valid point on the curve.

     var reduced[200] = reduce_overflow_signed_dl(CHUNK_SIZE, CHUNK_NUMBER, MAX_CHUNK_NUMBER, MAX_CHUNK_SIZE, in);
-    var div_result[2][200] = long_div_dl(CHUNK_SIZE, CHUNK_NUMBER_MODULUS, CHUNK_NUMBER_DIV - 1, reduced, modulus);
+    var div_result[2][200];
+    for (var i = 0; i < CHUNK_NUMBER_DIV; i++){
+        div_result[0][i] = 0;
+        div_result[1][i] = 0;
+    }

We believe that this attack can be extended also to PointOnTangent and PointOnLine, allowing an attacker to prove invalid curve operations, and potentially forge ECDSA signatures.

Recommendation. It is recommended that the Big Integer Library used for ECDSA Verification is either carefully reviewed for such issues and fixed, or it is replaced by a more mature implementation.

Client response. Client has acknowledged issues with Big Integer Library used for ECDSA Verification and is evaluating alternatives.

#03 - Exclusion Check Of Forbidden Countries Is Unsound And Incomplete Due To Incorrect Indexing

Severity: High Location: protocol circuits

Description. The ProveCountryIsNotInList template checks whether the country contained in the passport is not in a forbidden countries list, where each country is represented by a 3-letter country code.

The check is performed by iterating over forbidden countries entry and comparing each letter individually for equality, as seen in the snippet below.

signal input dg1[93];
signal input forbidden_countries_list[MAX_FORBIDDEN_COUNTRIES_LIST_LENGTH * 3];

signal equality_results[MAX_FORBIDDEN_COUNTRIES_LIST_LENGTH][4];
for (var i = 0; i < MAX_FORBIDDEN_COUNTRIES_LIST_LENGTH; i++) {
    equality_results[i][0] <== IsEqual()([dg1[7], forbidden_countries_list[i ]]);
    equality_results[i][1] <== IsEqual()([dg1[8], forbidden_countries_list[i + 1]]); 
    equality_results[i][2] <== IsEqual()([dg1[9], forbidden_countries_list[i + 2]]);
    equality_results[i][3] <==  equality_results[i][0] * equality_results[i][1];
    0 ===  equality_results[i][3] * equality_results[i][2];
}

However, the index i that is used to loop over the forbidden countries list is incorrect, as it should loop over i * 3 instead.

Impact. This issue breaks both soundness and completeness as demonstrated by the following examples: - Unsound: let MAX_FORBIDDEN_COUNTRIES_LIST_LENGTH = 3 and forbidden_countries_list = ["ABC","DEF","GHI"], then someone with the passport from GHI country will pass the check because the loop will stop at i = 3. - Incomplete: let forbidden_countries_list = ["ABC","DEF"], then someone with the passport from BCD country will not pass the check because the loop will also check over i = 2, i = 3, and i = 4.

Recommendation. Update the indexing of forbidden_countries_list to use i*3, as seen in the updated snippet below:

signal input dg1[93];
signal input forbidden_countries_list[MAX_FORBIDDEN_COUNTRIES_LIST_LENGTH * 3];

signal equality_results[MAX_FORBIDDEN_COUNTRIES_LIST_LENGTH][4];
for (var i = 0; i < MAX_FORBIDDEN_COUNTRIES_LIST_LENGTH; i++) {
    equality_results[i][0] <== IsEqual()([dg1[7], forbidden_countries_list[i * 3 ]]);
    equality_results[i][1] <== IsEqual()([dg1[8], forbidden_countries_list[i * 3 + 1]]); 
    equality_results[i][2] <== IsEqual()([dg1[9], forbidden_countries_list[i * 3 + 2]]);
    equality_results[i][3] <==  equality_results[i][0] * equality_results[i][1];
    0 ===  equality_results[i][3] * equality_results[i][2];
}

Client response. Client has acknowledged the issue and pushed changes to the main branch together with additional tests.

#04 - Second Pre-Image Attacks On PackBytesAndPoseidon May Be Used To Register Arbitrary Passports And DSC Certificates

Severity: High Location: protocol circuits

Description. The function PackBytesAndPoseidon(k) in CustomHashers.circom is susceptible to a second pre-image attack: given an input $x$ an input $y$ can be found such that PackBytesAndPoseidon(k)(x) == PackBytesAndPoseidon(k)(y) where $y$ is not an array of bytes, but an array of arbitrary field elements. For example consider $[0, 1, 0]$ and $[256, 0, 0]$ they both compute $[256]$ as an intermediate value (output of PackBytes in zk-email’s bytes.circom). This is because this function computes $\sum_{i}^{k} b_{i} * 2^{8 * i}$ for a given chunk of input bytes $b_{i}$ (chunks can be at most 31 bytes long to avoid overflowing the Circom order). This function is injective on a given chunk of bytes as long as the input respects the condition of being an array of values $[0, . ., 255]$ . If not, collisions can be easily found and is the aforementioned example.

This intermediate value is later passed to the CustomHasher function: because the intermediate value is identical, both inputs will yield the same hash. This vulnerability can be exploited for instance from register.circom by attacking the raw_dsc signal as follows: Assume an attacker has a legitimate raw_dsc that has already been checked for valid signature against a CSCA, so it is included in the Merkle tree. The attacker can modify bytes in the raw_dsc and the circuit will still compute the same signal

dsc_hash <== PackBytesAndPoseidon(MAX_DSC_LENGTH)(raw_dsc);

To illustrate a possible attack consider the following example. A legitimate raw_dsc (taking from the project tests) is modified in the first 2 bytes ("304","129" instead of "48","130"). This modified input, together with the original parameters passes the circuit witness generation and verification (in particular, it passes the inclusion check in the Merkle tree by exploiting the collision). More interestingly, modifying the first byte of the public key in byte $305$ of the original raw_dsc and the corresponding value in pubKey_dsc by changing it from "166" to "165" (and compensating accordingly in byte $304$ ). This input passes all constraints in the circuit up to before the passport verification, including CheckPubkeysEqual. It does not pass passport verification because the rest of the values in the input were not modified to match the new public key, for which we cannot easily compute the corresponding private key in this case.

Impact. This is a serious vulnerability because, although it is not possible for an attacker to modify all bytes of a key, given that some bytes outside the key are needed to preserve the hash collision, using this technique an attacker could modify up to 30 bytes of the original public key and search for a new public key he can factorize to sign an arbitrary passport. Similarly he could freely modify up to 30 bytes of an ECDSA key (which could be as small as 56 bytes for brainpool224) to achieve a similar goal of computing a corresponding valid private key. Moreover, given that a similar Merkle tree inclusion test is performed on dsc.circom to check for valid CSCA certificates, the same attack strategy could be performed there, this time attacking a valid and previously registered raw_csca with the goal of signing an arbitrary raw_dsc.

Recommendation. We recommend that the ranges of the bytes array are checked, either at the top level circuits (register.circom and dsc.circom) or inside PackBytesAndPoseidon, or both (defense in depth) to address this.

Client response. Client has acknowledged this issue and added a range check to the PackBytesAndPoseidon function in order to mitigate the potential overflow in the elements of the input array. To do this they have added the function AssertBytes that relies on LessThan. It has been noted that their fix can be simplified by using Num2Bits(8).

#05 - Trusting The Start Offset Of The Public Key Inside The Certificate May Lead To Signature Forgery And Invalid Passport Registration

Severity: High Location: protocol circuits

Description. All the checks of signatures in the circuits are performed by extracting the public key of the signer certificate, and then verifying the signature against this public key. The circuits, however, do not parse the certificate to locate the public key position, but instead trust the user to provide the correct offset. The rationale would be that an incorrect offset

This reasoning is however not sound: while it is somewhat reasonable for ECDSA public keys, it is not for RSA public keys. Recall that an RSA public key is a composite number $n = p \cdot q$ and a public exponent $e$ . The private key is the factorization $p, q$ and a private exponent $d$ which is computed as follows:

d = e^{- 1} \mod ϕ (n)

The security of RSA signatures relies on the fact that the public key $n$ is hard to factorize, and thus the private exponent $d$ is hard to compute.

Allowing an attacker to control the start offset of the public key in the certificate allows the attacker to potentially provide a signature with a public key that is not the one intended by the original signer. There is one notable case where signatures are easy to forge: if the public key is a prime number. In that case the private exponent is simply computed as

d = e^{- 1} \mod (n - 1)

and thus an attacker can forge arbitrary signatures.

Impact. This can be exploited for example by finding a CSCA certificate with a 2048-bit prime in their encoding. Since the probability of a random 2048-bit integer being a prime is roughly $1 / \log (2^{2048}) \approx 1 / 2048$ , and assuming that a certificate is typically around 2 kB, we are expected to find such a suitable certificate by examining a very small number of them. As an example the Italian CSCA certificate contains a 2048-bit prime at byte offset 821.

An attacker can then pass this offset to the DSC circuit to register an invalid DSC certificate, and this allows them to sign arbitrary passports.

Recommendation. It is recommended to correctly parse the certificate to locate the public key, and not trust the user to provide the correct offset.

Client response. Client has acknowledged the issue. They are evaluating to add a DER parsing implementation in Circom in the future, but are evaluating existing implementations with respect to their security. In the meantime, they have identified a heuristic to check for surrounding bytes to the declared public key position and have implemented this in https://github.com/zk-passport/openpassport/pull/358 for RSA. We believe that this heuristic partially mitigates the issue, but a more robust solution would be to use a DER parser that identifies the key position for both RSA and ECDSA. We think that, until such a thorough check is implemented, the heuristic can be made more robust by also looking for the Algorithm OIDs for both RSA and ECDSA and, in the case of RSA, for the public exponent to be next to the key.

#06 - Harden TEE Client and Server Communication

Severity: Medium Location: TEE client

Description. Currently, the connection between the TEE client and server is neither encrypted nor authenticated. The connection is made through hardcoded websocket URLs that use the ws protocol instead of the secure wss protocol:

export const WS_RPC_URL = "ws://54.71.75.253:8888/";
export const WS_URL = "ws://43.205.137.10:8888/";

The impact is limited as data is eventually signed and verified to come from a Nitro enclave, nevertheless it is better to prevent replays and MITM attacks by using a secure connection at least between the clients and the enclave host.

In addition, the enclave can technically be swapped for another enclave that is run by a malicious actor, as the client only verifies the image being run on the enclave and not that it is the “official” Self enclave. While this is a very unlikely attack vector as even a malicious Enclave would have to run the proper program (and thus would be unable to leak user data), it is still a good practice to verify the unique enclave ID deployed by Self.

Recommendation. Use the wss protocol for the websocket connection between the TEE client and server. In addition, consider verifying the unique enclave ID of the enclave running the Self program. From the documentation:

An enclave ID is a unique identifier across AWS. It consists of the parent instance ID and an identifier for each enclave created by the instance. For example, an enclave created by a parent instance with an ID of i-1234567890abcdef0 could have an enclave ID of i-1234567890abcdef0-enc9876543210abcde.

#07 - TEE Server Memory Grows Unbounded

Severity: Medium Location: TEE server

Description. The Nitro enclave deployed by Self uses an in-memory HashMap to store shared secrets with users. This store is never pruned or garbage collected and thus grows unbounded.

This means that the enclave can grow indefinitely, potentially crashing once it hits some memory limit. You can see this in the implementation of the store in src/store.rs:

pub struct HashMapStore {
    ecdh_store: HashMap<String, Vec<u8>>,
}

impl Store for HashMapStore {
    fn insert_new_agreement(
        &mut self,
        uuid: uuid::Uuid,
        shared_secret: Vec<u8>,
    ) -> Result<(), ring::error::Unspecified> {
        self.ecdh_store.insert(uuid.to_string(), shared_secret);
        Ok(())
    }

    fn get_shared_secret(&self, uuid: &String) -> Option<Vec<u8>> {
        self.ecdh_store.get(uuid).cloned()
    }
}

Not only this might become a problem naturally with time, but this is also something that malicious users could exploit to facilitate a Denial-of-Service attack on the enclave.

Furthermore, pruning older sessions provides forward-secrecy to the scheme, as shared secrets are derived from ephemeral key exchanges, preventing a break of the Nitro enclave from leaking past exchanges.

Recommendation. We recommend implementing a simple LRU cache to store the shared secrets. This would allow the enclave to keep only the most recent shared secrets and discard the older ones. This would also prevent the enclave from crashing due to memory exhaustion. In addition, sessions and their shared secrets could be deleted more aggressively from the store, for example when they are finalized by the creation of a proof.

Keep in mind that one might want to harden this measure by rate-limiting hello requests based on IP address alone in order to prevent one user from evicting honest sessions from other users.

#08 - The Big Integer Library Used For Ecdsa Verification Is Immature

Severity: Medium Location: dependencies circuits

Description. Big integer and foreign field emulation is one of the most critical components of the project, as it is used to check the validity of elliptic curve operations, and thus ECDSA signatures. We have identified several issues and oddities in the library, that indicate that it is not mature enough to be used in production, and should be reviewed and tested more thoroughly.

Range check is unconstrained

In the BigIntIsZeroModP template, the range check of the output is never enforced, as it is simply witnessed using <--. Additionally, it is not clear why this range check should be necessary at all.

// range checks
// why explained above
// TODO: research last chunk check, maybe less bits will be enough
component kRangeChecks[CHUNK_NUMBER_DIV];
for (var i = 0; i < CHUNK_NUMBER_DIV; i++){
    k[i] <-- div_result[0][i];
    kRangeChecks[i] = Num2Bits(CHUNK_SIZE);
    kRangeChecks[i].in <-- k[i]; // should be <==
}

Missing checks for the chunks wapping around the native field

Throughout the library, there is little to no check for wrap-around in the chunks over the native field. This is one of the most important aspects of a big integer library, as if there is wrap around, the integer operations are no longer sound, as illustrated by the following relation:

\sum_{i = 0}^{n} 2^{S \cdot i} \cdot c_{i} e q \sum_{i = 0}^{n} (2^{S \cdot i} \cdot c_{i} \mod p)

Intuitively, first wrapping around the native modulus, and then computing the linear combination of the chunks may yield a different integer than the one expected. Usually, to enhance performance, developers do not compute the normalized representation after each operation, but only at the end of a sequence of operations. However, care must be taken to ensure that the operations are still sound, and that the chunks do not overflow or underflow the native field. In the library, it is not clear how this is prevented (if at all), especially in the overflow operations.

Recommendation. It is recommended to carefully review the big integer library, taking extra care to ensure that the operations are sound and that the chunks do not wrap around the native field.

Client response. Client has acknowledged issues with Big Integer Library used for ECDSA Verification and is evaluating alternatives.

#0a - Off-By-One In Dsc Padding Check

Severity: Medium Location: protocol circuits

Description. There is an off-by-one bug in circuits/circuits/dsc/dsc.circom when checking the padding with raw_dsc_padded_length:

template DSC(
    signatureAlgorithm,
    n_csca,
    k_csca
) {
    // TRUNCATED...

    // check that raw_dsc is padded with 0s after the sha padding
    // this should guarantee the dsc commitment is unique for each commitment
    component byte_checks[MAX_DSC_LENGTH];
    for (var i = 0; i < MAX_DSC_LENGTH; i++) {
        byte_checks[i] = GreaterThan(12);
        byte_checks[i].in[0] <== i;
        byte_checks[i].in[1] <== raw_dsc_padded_length;

        // If i >= raw_dsc_padded_length, the byte must be 0
        raw_dsc[i] * byte_checks[i].out === 0;
    }

The position at offset raw_dsc_padded_length is not checked to be zero. This is because byte_checks[raw_dsc_padded_length].out will be set to 0 letting the last constraint pass for any value of raw_dsc[raw_dsc_padded_length].

This bug allows malicious users to produce 256 possible Merkle leaves to insert in the DSC Merkle tree from a single DSC.

Reproduction Steps. You can reproduce the issue using the following test:

it.only('should demonstrate that tampering raw_dsc[raw_dsc_padded_length] changes the DSC tree leaf without failing in the buggy circuit', async () => {
      // 1. Compute the witness with correct (untampered) inputs
      const goodWitness = await circuit.calculateWitness(inputs, false);
      await circuit.checkConstraints(goodWitness);
      const originalLeaf = (await circuit.getOutput(goodWitness, ['dsc_tree_leaf'])).dsc_tree_leaf;

      // 2. Tamper the input so that raw_dsc[raw_dsc_padded_length] is nonzero
      const tamperedInputs = JSON.parse(JSON.stringify(inputs));
      const paddedLength = Number(tamperedInputs.raw_dsc_padded_length);
      tamperedInputs.raw_dsc[paddedLength] = '255'; // or any nonzero value

      // 3. Recompute the witness. In the buggy circuit, this does NOT fail!
      //    In a fixed circuit, you'd get "Assert Failed" here.
      const tamperedWitness = await circuit.calculateWitness(tamperedInputs, false);
      await circuit.checkConstraints(tamperedWitness);
      const tamperedLeaf = (await circuit.getOutput(tamperedWitness, ['dsc_tree_leaf']))
        .dsc_tree_leaf;

      // 4. Log/compare the two leaves. They SHOULD be identical if the circuit truly enforced zero-padding;
      //    Instead, in the buggy circuit, they will differ, proving the malleability.
      console.log('Original DSC tree leaf:', originalLeaf);
      console.log('Tampered DSC tree leaf:', tamperedLeaf);

      // 5. Demonstrate that the leaf has changed
      expect(tamperedLeaf).to.not.equal(
        originalLeaf,
        'Leaf was changed by tampering, yet the circuit did not reject the proof'
      );
    });

Recommendation. Update the padding check to use GreaterEqThan instead of GreaterThan to ensure that the padding is correct.

#0b - Potential DoS Vector In TEE Server Hello Endpoint

Severity: Low Location: TEE server

Description. In the following “hello” endpoint of the TEE server, located in src/server.rs, a conversion is done on the uuid user request:

#[async_trait]
impl<S: Store + Sync + Send + 'static> RpcServer for RpcServerImpl<S> {
    async fn hello(
        &self,
        user_pubkey: Vec<u8>,
        uuid: uuid::Uuid,
    ) -> ResponsePayload<'static, HelloResponse> {
        // TRUNCATED...

        match sqlx::query("SELECT * from proofs WHERE request_id = $1")
            .bind(sqlx::types::uuid::Uuid::from_str(uuid.to_string().as_str()).unwrap())
            .fetch_one(&self.db)
            .await
        {

Since we are converting from a uuid::Uuid type to a sqlx::types::uuid::Uuid type, edge-cases in the different implementations might fail to properly convert the type and crash on specially-crafted user inputs (introducing a Denial-of-Service bug).

Recommendation. While we could not find a way to exploit this, we recommend edging on the side of caution and converting the unwrap to a proper error.

#0c - Missing Range Check On The Chunk Sizes In ECDSA

Severity: Low Location: dependencies circuits

Description. The template for ECDSA signature verification does not check whether the chunk size is smaller to the declared maximum chunk size. For instance consider the following input for the curve p256 with SHA256 where the second chunk of s is 125 bits instead of 64. This example passes signature verification.

{
  "curve": "p256",
  "signature": [
    [
      "11897043862654108222",
      "6687976630675743167",
      "6842677606991059234",
      "3933303995770833589"
    ],
    ["10364704208062614840", "21394470794141451286901280378935131115", "0", "15812853153589603704"]  ],
  "pubKey": [
    [
      "1647443686294582730",
      "7524809848328723651",
      "2690299118416708846",
      "2230381215521625212"
    ],
    [
      "12063856007545978738",
      "2856046104882309217",
      "14084651496056034469",
      "2603012891351374004"
    ]
  ],
  "hashParsed": [0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0]
}

Impact. This missing check allows an attacker to craft multiple representations of valid signatures (signature malleability). This does not pose an immediate threat to the overall protocol but could be an issue in future versions (for instance if signatures are used to compute nullifiers or the concrete representation is otherwise relevant for the protocol).

Recommendation. Check whether each chunk has at most CHUNK_SIZE bits to avoid multiple valid representations of valid signatures.

Client response. Client has fixed this issue in PR https://github.com/zk-passport/openpassport/pull/354. The fix addresses this issue using the custom isNBits function. It has been noted that an alternative and easier fix is to use the Circom-lib Num2Bits as it is done for the RSA PKCS verification circuits.

#0d - Missing Range Check In The Ecdsa Signature Component

Severity: Low Location: dependencies circuits

Description. In the ECDSA signature verification template, the signature components $(r, s)$ are not explicitly range-checked to ensure they fall within $[1, n - 1]$ , where $n$ is the order of the curve. This omission allows signatures of the form $(r, s + k \cdot n)$ to be incorrectly accepted as valid for any integer $k$ , provided the values remain within the maximum bit length.

Recommendation. Implement strict range-check to ensure that both $r$ and $s$ are explicitly validated to satisfy the condition:

1 \leq r \leq n

and $1 \leq s \leq n$

Client response. Client has addressed this in PR https://github.com/zk-passport/openpassport/pull/354. This relies on a copy of the BigLessThan function from the Big Integer library used for ECDSA verification. It has been observed that although we could not find immediate issues with that function, it is implemented in an unorthodox way (checking chunks from least significant to most significant, whereas for instance a similar function exists in the circom-bigint library checking in the opposite order). Client has acknowledged this and will use the BigLessThan from the zk-email library.

#0e - Over-Constraint In Ecdsa For Large x1 Coordinate

Severity: Low Location: dependencies circuits

Description. The implementation in the ECDSA circuit template does not perform a reduction modulo the curve order before computing the last comparison against the supplied r parameter:

    // x1 === r
    for (var i = 0; i < CHUNK_NUMBER; i++){
        add.out[0][i] === signature[0][i];

    }

This causes that a valid signature, where in the computation of the left-hand-side add.out[0][i] the value of x1 overflows the curve order, there will not be a chunk-by-chunk match as expected and the signature will be rejected. See for example the following test vector, taken from the Wycheproof dataset for p256 with SHA256. This signature is considered valid by OpenSSL, but rejected by the corresponding ecdsa.circom.

{
  "curve": "p256",
  "signature": [
    [
      "884452912994769579",
      "4834901530490986875",
      "0",
      "0"
    ],
    [
      "17562291160714782030",
      "13611842547513532036",
      "18446744073709551615",
      "18446744069414584320"
    ]
  ],
  "pubKey": [
    [
      "12004473255778836739",
      "5567425807485590512",
      "4612562821672420442",
      "781819838238377577"
    ],
    [
      "2517678904895060574",
      "13415238991415823444",
      "5824794594647846510",
      "14195660962316692941"
    ]
  ],
  "hashParsed": [1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1]
}

Impact. Users with valid passports where this corner case occurs in the signature will not be able to use the Self protocol since their signature will be considered invalid.

Recommendation. Perform a reduction modulo the curve order on the x1 variable (add.out) before comparing with the supplied r.

Client response. Client has addressed this issue in the PR https://github.com/zk-passport/openpassport/pull/354 by performing a reduction modulo the curve order before comparing with the right hand side r in the final comparison operation.

#0f - Over-Constraint In Ecdsa For Point Duplication

Severity: Low Location: dependencies circuits

Description. The ECDSA circuit template rejects a valid signature in the case of addition component add = EllipticCurveAdd(CHUNK_SIZE, CHUNK_NUMBER, A, B, P); for the same point (duplication). This is because the implementation of EllipticCurveAdd is using the slope $λ = (y 2 - y 1) / (x 2 - x 1)$ assuming two distinct points and is not checking if the points are equal (which triggers a division by 0).

See for example the following test vector, taken from the Wycheproof dataset for p256 with SHA256. This signature is considered valid by OpenSSL, but rejected by ecdsa.circom.

{
  "curve": "p256",
  "signature": [
    [
      "426272148761560425",
      "10109082184959048894",
      "10367380190526216452",
      "8008323498388584069"
    ],
    [
      "5572065651256165739",
      "4850669060902739298",
      "11049482860550425644",
      "13506970795533374378"
    ]
  ],
  "pubKey": [
    [
      "1014237914705717603",
      "7603118795020062695",
      "9465023375885712875",
      "6593603921886509673"
    ],
    [
      "5626662404605757929",
      "4059164823052520333",
      "22116508238925654",
      "9478459776621908713"
    ]
  ],
  "hashParsed": [1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1]
}

Impact. Users with valid passports where this corner case occurs in the signature will not be able to use the Self protocol since their signature will be considered invalid.

Recommendation. Consider and fix this case in the implementation of EllipticCurveAdd(CHUNK_SIZE, CHUNK_NUMBER, A, B, P); and use the correct slope for point duplication.

Client response. Client has acknowledged this issue. Given that the issue is on the implementation of ECDSA library done by an external team, they have forwarded the issue to them.

#10 - Over-Constraint In ECDSA For Edge Case In Scalar Multiplication

Severity: Low Location: dependencies circuits

Description. The ECDSA circuit template rejects a valid signature for an edge case on the scalar multiplication scalarMult1 = EllipicCurveScalarGeneratorMult(CHUNK_SIZE, CHUNK_NUMBER, A, B, P); which is computing u1 = h * s_inv * G.

See for example the following test vector, taken from the Wycheproof dataset for p256 with SHA256. This signature is considered valid by OpenSSL, but rejected by ecdsa.circom.

{
  "curve": "p256",
  "signature": [
    [
      "18446744073709551613",
      "18446744073709551615",
      "18446744073709551615",
      "9223372036854775807"
    ],
    [
      "1728225092527813315",
      "12329340899243473632",
      "12865806500782059869",
      "9367457946533734037"
    ]
  ],
  "pubKey": [
    [
      "10008439133547667927",
      "5411563034733612626",
      "15771927984209908287",
      "15930294780321765421"
    ],
    [
      "13667945291748886015",
      "16484076607543923488",
      "16958808623021268928",
      "13811779394532163557"
    ]
  ],
  "hashParsed": [1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1]
}

Impact. Users with valid passports where this corner case occurs in the signature will not be able to use the Self protocol since their signature will be considered invalid.

Recommendation. Consider and fix this corner case in the implementation of EllipicCurveScalarGeneratorMult(CHUNK_SIZE, CHUNK_NUMBER, A, B, P);.

Client response. Client has acknowledged this issue. Given that the issue is on the implementation of ECDSA library done by an external team, they have forwarded the issue to them.

#11 - Missing Range Check On The Chunk Sizes In RSA-PSS

Severity: Low Location: dependencies circuits

Description. The implementation in both versions of the circuit is not checking whether the chunk size is smaller to the declared maximum chunk size. For instance consider the following input for rsapss_sha256_3_2048 with salt length 64, where the first chunk has size 123 bits, although the declared maximum chunk size for this configuration is 120 bits. This example passes signature verification.

{
  "signature": ["7731115078616803665798114145181535098", "163203956634050319114380978254630080", "346148465904621811693353377067303234", "64964293608834970395530903389524729", "335420826842907861754475597205951544", "925528679415886357007293672250413399", "839020387053516695975203231151634658", "778568500012672705243235513963101764", "1237818354950660153047639164514793540", "1279126110528363299554438433474920526", "1271457987192236182994923269736835892", "988175487321830418383164411072850446", "887908374708917746102974749377227834", "209746796442816091240476041947465923", "1304363295406083456667488431125879054", "524718671036833927121760315388886895", "753317262042764462315754015065545818", "121", "0", "0", "0", "0", "0", "0", "0", "0", "0", "0", "0", "0", "0", "0", "0", "0", "0"],
  "modulus": [
    "466890184860597456401263469298030355",
    "934892081549427649323807927922900130",
    "208645761278164609062745855133745252",
    "706235177207591471475050602074473379",
    "292598569458658692052640890836570796",
    "495350572662119637520831264600583776",
    "1195022894548414203114969601950177119",
    "332800708856449316235710513302701152",
    "45000490396361335068087327257520852",
    "111185801182984893004870674922017989",
    "421368615499870239882744392415817086",
    "827966678350734062885488434550136996",
    "77942854540484756138148180622094839",
    "1043984843798011423344204006579183000",
    "1118402313189367453676081212715001540",
    "550698616548662574616349662954124741",
    "904303165189377290183430808673064367",
    "188",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0"
  ],
  "message": [1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 1]
}

Recommendation. Check whether each chunk has at most CHUNK_SIZE bits to avoid multiple valid representations of valid signatures.

Client response. Client has acknowledged the issue and fixed it in PR https://github.com/zk-passport/openpassport/pull/360/files. They have implemented a custom isNBits function for this purpose. It has been noted that it would be simpler to use Num2Bits, similarly as they do to check chunk sizes in the RSA PCKS circuit.

#12 - Missing Constraint On The Padding In RSA-PSS

Severity: Low Location: dependencies circuits

Description. In the RSA-PSS padding verification, the last byte of the message is checked to be 0xbc using an assert call.

    //should end with 0xBC (188 in decimal)
    assert(eM[0] == 188);

This is required in the fourth step of the verification algorithm (from the RFC)

If the rightmost octet of EM does not have hexadecimal value 0xbc, output “inconsistent” and stop.

However, the assert statement is not a constraint, and it is not enforced in the circuit. This means that the circuit will not fail if the last byte of the message is not 0xbc.

Impact.

An attacker can make a signature with an invalid padding be accepted by the circuit, because the last byte is essentially unconstrained. We believe that this has no practical impact on the security of the verification algorithm, but we still recommend fixing to me compliant with the specification.

Recommendation We recommend replacing the assert with a constraint that checks the last byte of the message to be 0xbc.

     //should end with 0xBC (188 in decimal)
-    assert(eM[0] == 188); 
+    eM[0] === 188;

Client response. Client has fixed this issue in commit https://github.com/zk-passport/openpassport/commit/6ad6f7fe2b1d5049aa17d0ecdb4a4d9097aeee3c.

#13 - Missing Range Check On The Signature In RSA-PSS

Severity: Low Location: dependencies circuits

Description. The implementation in both versions of the circuit is not checking whether the input signature is smaller to the modulus. For instance consider the following input for rsapss_sha256_3_2048 with salt length 64, where the signature is generated computing $s i g n a t u r e^{'} = s i g n a t u r e + m o d u l u s$ for a valid $s i g n a t u r e$ . This example is reject by OpenSSL but passes the circuit verification in Self.

{
  "signature": [
    "448593004166146035435698857233297481",
    "645183938101488623213176183413849323",
    "666034718174307596971224365157466704",
    "1271375153014817405982734151086452096",
    "1180028692934487107976994982225874491",
    "43804972648824013081797601863424227",
    "242516006679401681063343065419167823",
    "1182227289007376475828724611303448394",
    "901331680040946404805569866222078428",
    "1112202048195884255403471214134025563",
    "141640114810700046171697631501252046",
    "1319213481608985222605784359236670013",
    "1291596147188972332688115034547946543",
    "1255959259511537862873460606790747882",
    "1179627418594555107027925239956205308",
    "1278704611743277638652199540388493869",
    "286500237759217977031993526159467836",
    "298",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0"
  ],
  "modulus": [
    "424995376221342323916068129274876411",
    "67032731905523875217374208431095706",
    "1088902097090709882045251159028487271",
    "905520378129685131655683371940143205",
    "772653984210635001119928127332075925",
    "453720758617437459118995325060964811",
    "682423291494784049924695549058692937",
    "787266768752181208854233249088291469",
    "186472877058417959779133158879134681",
    "464686717810020849123595839870153012",
    "172023685318598391521750104755663284",
    "515549827144062588662785848942123249",
    "558628673475731478847640300679590539",
    "92387777511544778109146896322836204",
    "1061966765604557646220482768986492741",
    "551767739591461330436511362339519451",
    "394444902710212854489591990203694934",
    "221",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0"
  ],
  "message": [1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0]
}

Recommendation. Implement the range check for the signature in both templates as required by the specification and commonly implemented by signature verification libraries such as OpenSSL.

Client response. Client has added a range using BigLessThan in https://github.com/zk-passport/openpassport/pull/360/files.

#14 - Multiple Missing Constraints On The Padding In RSA-PSS

Severity: Low Location: dependencies circuits

Description. The implementation in both versions of the circuit is missing the constraints defined by step 10 of https://datatracker.ietf.org/doc/html/rfc8017#section-9.1.2:

If the emLen - hLen - sLen - 2 leftmost octets of DB are not zero or if the octet at position emLen - hLen - sLen - 1 (the leftmost position is “position 1”) does not have hexadecimal value 0x01, output “inconsistent” and stop.

This causes the current implementation to accept a signature with an invalid padding which is rejected by other standard implementations such as OpenSSL. For instance we have crafted the following example, for rsapss_sha256_3_2048 with salt length 64, with an incorrectly padded signature, that yet passes the signature verification.

{
  "signature": [
    "259352181564574862143578171312565797",
    "956499227725763736504359950019371303",
    "879104553708082061777004523508957070",
    "1273288609027626641777651316182319346",
    "673678469906704059893509971132768301",
    "856473360535849873833520678123825331",
    "825425390774804518752322087283828831",
    "4302740523185230558121823473793809",
    "199256958749154701239837132259350076",
    "110306654933022706627356373564557292",
    "1192611112869568006075994762353805292",
    "1079713868370030632647205956774097623",
    "332146788580611472993358578544154516",
    "1095988428794885025005638929447969118",
    "927398408271425673797287519988389870",
    "1103999881772553827448853812384637597",
    "1001019711001236589959717395725420927",
    "89",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0"
  ],
  "modulus": [
    "166971367507381150908725724332053273",
    "338834395979712676423550659442119092",
    "990122998959864087711595965672871220",
    "494484934473321533400781405965416851",
    "270389147833210877695698176151741372",
    "1125145922868136508551852559151444462",
    "384891297666414462051112916771801150",
    "804556834408335038110950013904794388",
    "32985675228989000004957020130689419",
    "1049312509536686136209605655944870072",
    "841612905868130386489153460440472540",
    "389417081829771264821648038620806323",
    "40657089948473049151954509221179812",
    "836060646953832634833744389761571273",
    "1096854257979362469517000714698821835",
    "92378592340849359218710031963837338",
    "45669349180999618770144486031940097",
    "162",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0",
    "0"
  ],
  "message": [1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1]
}

Impact.

An attacker can make a signature with an invalid padding be accepted by the circuit. An incorrectly implemented padding checking is not conformant with respect to the specification, and invalidates the security guarantees of the padding scheme. Although it is not trivial to exploit this vulnerability, under some circumstances errors in implementations may result in major attacks such as signature forgeries therefore we recommend to correctly implement these constraints.

Recommendation Implement the constraints defined in step 10 of https://datatracker.ietf.org/doc/html/rfc8017#section-9.1.2 for both templates.

Client response. The constraints related to Step 10 have been added to both circuits in PR https://github.com/zk-passport/openpassport/pull/331/files.

#15 - Wrong Ceil Division in Message Chunk Computation

Severity: Low Location: protocol circuits

Description. The SignatureVerifier template computes the number of n-bit chunks for the hash using the expression:

msg_len = (HASH_LEN_BITS + n) \ n

When HASH_LEN_BITS is an exact multiple of n (e.g. 256 bits with chunks of 32 bits), this results in an extra chunk (e.g. 9 chunks instead of 8). Consequently, downstream, the extra (unnecessary) chunk is used to populate the message array for RSA signature verifiers. This could lead to an unsound signature verification if the extra chunk is unconstrained or incorrectly processed by the underlying verification circuit.

Recommendation. Change the computation of msg_len to use the correct ceiling formula:

var msg_len = (HASH_LEN_BITS + n - 1) \ n;

#16 - Consider Making TEE Attestations More Auditable

Severity: Informational Location: TEE client

Description. By using Nitro enclaves, Self provides users with some assurance on the code that handles the client’s secret data during the proof delegation flow.

However, these assurances take their full value only when clients attempt to verify the validity of the (open source) code that will be run within the enclave.

Verifying the TEE code is not enough, a client who wants to ensure that the code running in the enclave is the one they expect must also:

verify that the enclave was deployed with the correct image by being able to reproduce the image hash and compare it with the measurements provided by the enclave’s attestation
verify that the code that they are running correctly verify that enclave attestation

One part of the answer is to ensure that the image being built and deployed in the enclave is reproducible. Currently the Dockerfile used for that does not encode any of the dependency versions it installs, making this process more difficult.

Another part of the answer is to make the client code more auditable. For example, the root AWS certificate is hardcoded in app/src/utils/proving/awsRootPem.ts as:

export const AWS_ROOT_PEM = `
-----BEGIN CERTIFICATE-----
MIICETCCAZagAwIBAgIRAPkxdWgbkK/hHUbMtOTn+FYwCgYIKoZIzj0EAwMwSTEL
MAkGA1UEBhMCVVMxDzANBgNVBAoMBkFtYXpvbjEMMAoGA1UECwwDQVdTMRswGQYD
VQQDDBJhd3Mubml0cm8tZW5jbGF2ZXMwHhcNMTkxMDI4MTMyODA1WhcNNDkxMDI4
MTQyODA1WjBJMQswCQYDVQQGEwJVUzEPMA0GA1UECgwGQW1hem9uMQwwCgYDVQQL
DANBV1MxGzAZBgNVBAMMEmF3cy5uaXRyby1lbmNsYXZlczB2MBAGByqGSM49AgEG
BSuBBAAiA2IABPwCVOumCMHzaHDimtqQvkY4MpJzbolL//Zy2YlES1BR5TSksfbb
48C8WBoyt7F2Bw7eEtaaP+ohG2bnUs990d0JX28TcPQXCEPZ3BABIeTPYwEoCWZE
h8l5YoQwTcU/9KNCMEAwDwYDVR0TAQH/BAUwAwEB/zAdBgNVHQ4EFgQUkCW1DdkF
R+eWw5b6cp3PmanfS5YwDgYDVR0PAQH/BAQDAgGGMAoGCCqGSM49BAMDA2kAMGYC
MQCjfy+Rocm9Xue4YnwWmNJVA44fA0P5W2OpYow9OYCVRaEevL8uO1XYru5xtMPW
rfMCMQCi85sWBbJwKKXdS6BptQFuZbT73o/gBh1qUxl/nNr12UO8Yfwr6wPLb+6N
IwLz3/Y=
-----END CERTIFICATE-----`;

It would be useful to mention that the data came from https://docs.aws.amazon.com/enclaves/latest/user/verify-root.html#validation-process so that users can more easily audit the source code.

#17 - Smart Contracts Are Not Following Some Solidity Coding Standards

Severity: Informational Location: contracts

While the smart contracts accurately follow the Solidity style guide, there are a few possible adjustments that would improve code quality even further.

Pragma directives should be fixed to clearly identify the Solidity version with which the contracts will be compiled. To improve reliability and avoid unintended issues caused by differences between compiler versions, consider using a fixed pragma directive, e.g., instead of pragma solidity ^0.8.28, use pragma solidity 0.8.28. The only exception to this rule are Solidity libraries or “library-like” contracts, such as OpenZeppelin’s and Solady’s contracts. In these special cases, the pragma should not be fixed because it is usually unclear which compiler version the end user of the library will be using.

Named imports are used quite a lot throughout the codebase. However, they are not always used consistently. For example, PassportAirdropRoot.sol uses a named import for the circuit constants

import {CircuitConstants} from "../constants/CircuitConstants.sol";

while IdentityVerificationHubImplV1.sol does not:

import "./constants/CircuitConstants.sol";

Admittedly, using or not using a named import does, in many cases, not make a difference. However, named imports are generally considered the better pattern. The reason is that if multiple contracts or libraries are defined inside the imported file, it is possible to unnecessarily pollute the namespace. This can lead to dead code if the compiler optimizer does not remove it (which is sometimes the case). So, unless there is a good reason not to use them, named imports should be preferred and applied consistently throughout the codebase.

Several functions of the contracts in scope could benefit from more extensive input validation. To give one example, the formatDate function of the Formatter library only checks the date string’s length but does not verify validity, i.e., it does not check if the values for day, month, and year actually correspond to a reasonable date. Several other functions of the smart-contract codebase could similarly be made more robust by improving input validation using requirements like zero-address checks, etc.

Client response. Fixed the version pragmas of all non-library contracts, applied named imports consistently, and added more extensive input validation in this pull request.

← Back to Index