Audit of Aleph Zero Shielder

March 25th, 2025 • Technical Report

Introduction

On March 25th, 2025, zkSecurity was tasked to audit the Aleph Zero Shielder project. The specific code to review was shared via a public repository (https://github.com/Cardinal-Cryptography/zkOS-monorepo at commit 22e2f52) and a private repository (zkOS-circuits at commit 491a0dd). The audit lasted 2 weeks with 2 consultants.

The code was found to be clean and well tested. A few observations and findings have been reported to the Aleph Zero team, which are detailed in the following sections.

Scope

The scope of the audit included the following components:

The Shielder protocol circuits. This part consisted of the circuits for account creation, deposit, withdrawal and Merkle proof verification. This logic was located in zkOS-circuits/crates/shielder-circuits/src.

Solidity smart contracts. This part included the contract handling business logic (in zkOS-monorepo/contracts) and the script to generate solidity assembly code for the Poseidon2 hash (in zkOS-monorepo/poseidon2-solidity).

Client SDK written with Rust and TypeScript. This part included the Rust crates for the typescript client (zkOS-monorepo/crates/shielder_bindings, zkOS-monorepo/crates/shielder-account, and zkOS-monorepo/crates/type-conversions) and the typescript client packages (zkOS-monorepo/ts/shielder-sdk/src, zkOS-monorepo/ts/shielder-sdk-crypto, and zkOS-monorepo/ts/shielder-sdk-crypto-wasm).

The Halo2 verifier in the contract and the Poseidon2 component in the circuit are not within the scope of this audit.

Overview

Overview of the Shielder Protocol

The Shielder is a zcash-like shielded pool run on EVM chains. It allows users to deposit and withdraw their tokens (including ERC20 token and Native token) with privacy. The relation among these deposits and withdrawals is hidden by default. In order to protect the Shielder from bad actors, the protocol introduces the Anonymity Revoker that can reveal the activity of an account when necessary (e.g., when a hacker is depositing illicit funds).

At a high level, the Shielder is a smart contract that holds all the users’ deposited funds. The ownership of these funds is not publicly revealed. Instead, the contract accepts deposits and withdrawals by verifying Zero Knowledge Proofs in Halo2. From the user’s perspective, they can create their own accounts in the Shielder, deposit, and withdraw freely from the accounts by generating the proof. For every deposit/withdrawal transaction, others won’t learn which account it’s interacting with.

Note

The core data structure in Shielder is the Note, representing the state of an account. It’s held by the account owner and not publicly revealed.

#[derive(Copy, Clone, Debug)]
pub struct Note<T> {
    pub version: NoteVersion,
    pub id: T,
    pub nullifier: T,
    pub trapdoor: T,
    pub account_balance: T,
    pub token_address: T,
}

When a user deposits or withdraws a token in the protocol, it will consume the old Note (old account state) and create a new Note (new account state). For example, when a user deposits a 100 unit of token into the account, the circuit will add 100 to the account_balance and thus create a new Note. The circuit ensures that the transition is valid.

Let’s go through each field one by one:

version represents the protocol version, currently always 0.
id is the unique identifier of an account. When a user deposits/withdraws, the id between the old Note and new Notes are always the same (but still private). The id here helps to track the transitions of an Account when necessary (more on this later).
nullifier is used to invalidate the consumed Note. During the Note transition, the circuit will calculate hash_old_nullifier = hash(old_nullifier) and make the hash_old_nullifier public. The smart contract will add the hash_old_nullifier to a global set and ensure there is no duplicate hash_old_nullifier. As the hash_old_nullifier is deterministically derived from old_nullifier, this ensures that a Note can only be spent once. The user always needs to set a new nullifier for new Note. This is a common pattern used in the shielded pool like Zcash and Tornado Cash.
trapdoor acts like a “private key”. Only the user who holds the trapdoor can spend the Note. This is because the user can only create a valid proof with the trapdoor value (as well as other fields in the Note). During the Note transition, the user can either set a new trapdoor or keep the same trapdoor in the Note.
token_address is the token address that this account holds. One account can only hold one type of token, which is either native token (e.g., ETH on Ethereum Mainnet) or ERC20 token. The token address will stay the same during Note transition.
account_balance is the balance of the account. During deposit/withdrawal transition, the circuit will constrain old_account_balance + delta_amount = new_account_balance, where delta_amount is the public deposit/withdrawal amount.

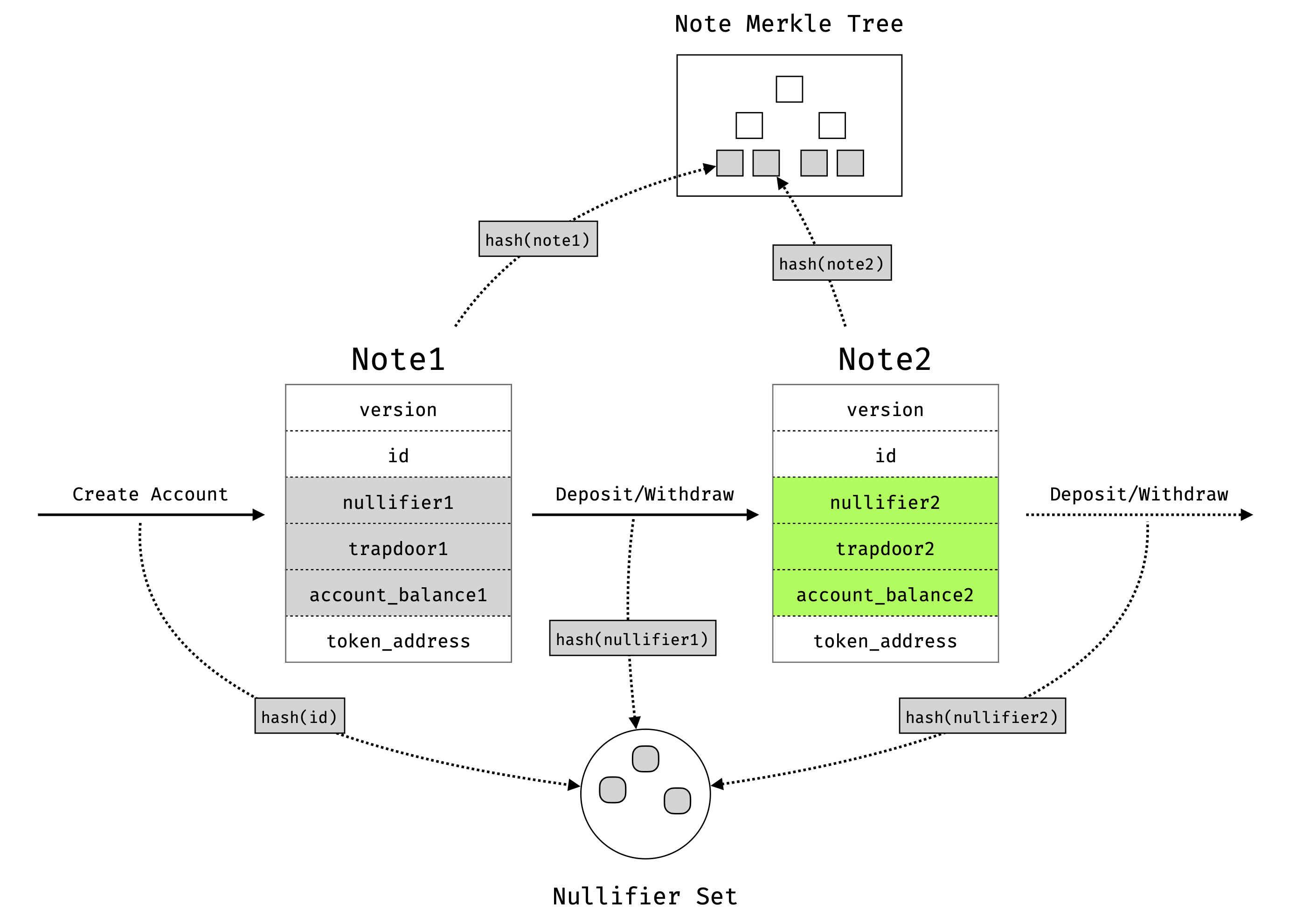
note-transition

During the Note transition, the protocol needs to ensure the user is spending a valid Note. This is achieved by checking (a.) the Note exists in the system and (b.) it hasn’t been consumed yet. The latter is enforced by the nullifier described above. The former is achieved using a Merkle tree proof.

Every time a new Note is created (either via account creation or deposit/withdrawal), the circuit calculates the new note hash note_hash = hash(note) and emits it. The contract will insert the note_hash to a global note hash Merkle tree. During a deposit/withdrawal transaction, the circuit enforces the spending note hash exists in the Merkle tree. This ensures that the spending Note must exist in the system (i.e., must be created by a prior transaction). As the Merkle check is in the circuit, others won’t learn the exact note hash value or its position in the Merkle tree. Thus the others won’t know which exact Note it is spending. That is, “We know the transition is valid but We don’t know which account it is handling”.

Anonymity Revoker

An innovative part of the Shielder is to introduce Anonymity Revoker to track the account when necessary.

By design, in the Note transition, the id is never changed. The idea here is to enable the Anonymity Revoker to “decrypt” the id in each transition. Here is how to do that:

Each account has a viewing key derived from id: viewing_key = hash(id, "key for AR"). As the id of an account is never changed, so is the viewing_key. When the account is created, the viewing_key is encrypted using Anonymity Revoker’s public key and the ciphertext is emitted. Then the Anonymity Revoker can decrypt the ciphertext to get the viewing_key. As a result, the Anonymity Revoker is able to collect the viewing_key of all accounts.
During each deposit/withdrawal transition, the account will emit a mac that commits the viewing_key of the account. The mac is computed as (r, hash(r, viewing_key)). The first part r is a random value, the second part is the hash of the random value r and viewing_key. Although this doesn’t directly reveal the viewing_key, it enables us to verify if the mac belongs to a given viewing key. For example, given a mac that has value (m1, m2), we want to check if it is emitted by the viewing key vk. We just need to check if m1 == hash(m2, vk). If yes then the transition is associated with the vk. That means, given a vk, we can scan all the transitions in history to match the transitions that belong to the vk. In that way we can reveal all the transitions of a vk.
If the Anonymity Revoker finds a malicious transition from a bad actor (for example, a hacker deposited the illicit fund into an account), it first reveals the viewing_key of the transition. They do this by trying every viewing key (collected in step 1) to match the mac of the transition. Once found the viewing_key, it just makes it public. Then everyone else is able to verify that the viewing_key is correct and use it to enumerate every transition to extract these transitions that belong to the viewing_key. This approach makes all the transactions of the bad actor become linkable.

Some notes for the protocol:

The Anonymity Revoker has to decrypt all viewing_key in account creation transactions to reveal one bad account. To ease this burden, one possible way is to encrypt the viewing_key in every transaction (including deposit/withdrawal). In this way the Revoker will only need to decrypt one single viewing_key to track the bad account. However, this will introduce a larger circuit in deposit/withdrawal and lead to a longer proving time.
Currently the revoker key is never changed. The key can decrypt all the transactions in history. Another possible way is to rotate the revoker key—say, once a month—and destroy the old key one month after it is revoked. If a transaction is found to be bad within one month, the Revoker just decrypts the transaction with the key. After one month the Revoker destroys the key and ensures all the previous transactions are not decryptable anymore. This achieves better privacy for the users because their transactions will eventually become fully private. This will also simplify the revoker key management because the Revoker doesn’t need to backup one key forever. It can even just generate the key in a secure enclave and make sure the key never leaves the hardware. Note that, to ensure the Revoker can decrypt an account with a new key, we still need to encrypt the viewing_key in every transaction.
One might think that during the Note transition, we can directly emit old_nullifier instead of calculating the hash. Unfortunately, this will lead to account locking issues. In that case the old_nullifier will be publicly included in the transaction. Others can frontrun the user’s transaction to set the same old_nullifier in the Note and consume it. Then the old_nullifier will be inserted to the global set and the user won’t be able to consume the original Note anymore.
The random r of the mac is freely chosen by the user. If two transitions emit two mac that have the same r but different commitment, then we know that they have different viewing keys and thus are from different accounts.

Shielder Circuits

The Shielder system under review consists of three main circuits new_account, deposit, and withdraw. They are implemented on top of a custom framework based on a PSE fork of Halo2. These circuits rely on several building blocks:

ElGamalEncryptionChip: Handles ElGamal encryption for the viewing key, requiring scalar multiplication and point addition on the Grumpkin curve.
RangeCheckChip: Ensures a balance does not underflow or overflow its intended range.
MerkleCircuit: Verifies Merkle inclusion proofs for notes.
NoteChip: Generates note hashes, enforces balance constraints, and checks the note version.
MacChip: Ensures the mac commitment is derived from the viewing key.
PoseidonCircuitHash: Calculates the hash in circuit, which is outside the scope of this audit.

Custom Framework

The custom framework atop Halo2 aims to simplify circuit composing by providing a structured way to defined gates:

Gate Trait. Each custom gate implements a Gate trait specifying the gate’s inputs, advice columns, and constraints, and how the gate should be synthesized with the inputs.
Column Pool. A shared ColumnPool automatically manages advice columns. Instead of manually declaring columns, the framework picks the least-used columns during synthesis to distribute assignments evenly and avoid “hot spots”, aiming to reduce circuit size. The pool tracks column usage and must remain stateful between configure and synthesize phases. Hence, it uses phase flags (ConfigPhase, PreSynthesisPhase, SynthesisPhase) to safeguard the needs of cloning when passing the pool between Halo2’s configuration and synthesis steps.

Scalar Multiplication

The Elliptic Curve scalar multiplication is needed for the ElGamal encryption. The circuit encodes the scalar value as a bit vector of fixed size. For each scalar bit, it applies constraints to ensure the correctness of the scalar multiplication process.

Scalar Bits Representation: A scalar is represented by bits ${b_{0}, b_{1}, \dots, b_{w - 1}}$ , where $w$ is the bit length. Each bit $b_{i}$ satisfies $b_{i} \cdot (b_{i} - 1) = 0$ , ensuring $b_{i} \in {0, 1}$ .

Double-and-Add Structure:In each step $i$ , two projective points are present in the circuit:

{i n p u t}_{i} = (x_{i}, y_{i}, z_{i})

{r e s u l t}_{i} = (X_{i}, Y_{i}, Z_{i})

We define:

{a d d e d}_{i} = {i n p u t}_{i} + {r e s u l t}_{i}

{d o u b l e d}_{i} = 2 \cdot {i n p u t}_{i}

Conditional Add: Accumulate the input to the result if the scalar bit is non-zero.
${r e s u l t}_{i + 1} = {r e s u l t}_{i} + b_{i} ({a d d e d}_{i} - {r e s u l t}_{i}) .$

Equivalently:

- If <math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mi>b</mi><mi>i</mi></msub><mo>&#x0003D;</mo><mn>0</mn></mrow></math>, <math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mrow><mi mathvariant="bold">r</mi><mi mathvariant="bold">e</mi><mi mathvariant="bold">s</mi><mi mathvariant="bold">u</mi><mi mathvariant="bold">l</mi><mi mathvariant="bold">t</mi></mrow><mrow><mi>i</mi><mo>&#x0002B;</mo><mn>1</mn></mrow></msub><mo>&#x0003D;</mo><msub><mrow><mi mathvariant="bold">r</mi><mi mathvariant="bold">e</mi><mi mathvariant="bold">s</mi><mi mathvariant="bold">u</mi><mi mathvariant="bold">l</mi><mi mathvariant="bold">t</mi></mrow><mi>i</mi></msub></mrow></math>.  
- If <math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mi>b</mi><mi>i</mi></msub><mo>&#x0003D;</mo><mn>1</mn></mrow></math>, <math xmlns="http://www.w3.org/1998/Math/MathML" display="inline"><mrow><msub><mrow><mi mathvariant="bold">r</mi><mi mathvariant="bold">e</mi><mi mathvariant="bold">s</mi><mi mathvariant="bold">u</mi><mi mathvariant="bold">l</mi><mi mathvariant="bold">t</mi></mrow><mrow><mi>i</mi><mo>&#x0002B;</mo><mn>1</mn></mrow></msub><mo>&#x0003D;</mo><msub><mrow><mi mathvariant="bold">a</mi><mi mathvariant="bold">d</mi><mi mathvariant="bold">d</mi><mi mathvariant="bold">e</mi><mi mathvariant="bold">d</mi></mrow><mi>i</mi></msub></mrow></math>.

The reason why not to constrain instead

{r e s u l t}_{i + 1} = {r e s u l t}_{i} + b_{i} \cdot {i n p u t}_{i}

is because the elliptic curve arithmetic constraints are only enforced to the “inner” expressions ${a d d e d}_{i}$ and ${d o u b l e d}_{i}$ , while the “outer” constraints, as shown in the conditional add above, cancels out the ${r e s u l t}_{i}$ to enforce the value of ${a d d e d}_{i}$ , if the scalar bit is 1.

Double: Doubles the input for the next step.
${i n p u t}_{i + 1} = {d o u b l e d}_{i} .$

Enforcing EC Arithmetic: The constraint expressions ${a d d e d}_{i}$ and ${d o u b l e d}_{i}$ , uses Algorithms 7 and 9 from [BCMS15] respectively.

ElGamal Encryption

The ElGamal encryption relies on the Grumpkin curve $y^{2} = x^{3} - 17$ . Given an Anonymity Revoker’s private key $a$ , an account’s private key $b$ (an independent random value), plaintext $m$ (point on curve), and generator $g$ :

Public key: $h = a \cdot g$
Shared key: $s = b \cdot h$
Ciphertext: $(c_{1}, c_{2}) = (b \cdot g, m + s)$

The circuit use ScalarMultipleChip to check $c_{1}$ that involves scalar multiplications, and use PointsAddChip to check $m \cdot s$ that involves point additions.

Note that a message can map to two points $(x, y)$ or $(x, - y)$ , but only the $x$ -coordinate matters for the viewing key.

Merkle Inclusion Proof

The Merkle tree has arity 7 and 14 levels (including the root). Proving a leaf’s inclusion requires verifying membership at each level up to the claimed Merkle root.

Membership Gate

A single “needle” value must appear in a “haystack” set of size $N$ . The product

\prod_{j = 1}^{N} (needle - {haystack}_{j})

is zero if and only if $needle$ is in the set.

Synthesis in a Merkle Chip:

Merkle Path Verification. Each level’s nodes(including the current node and sibling nodes) form the haystack, and the current node is the needle.
Membership Gate. Enforced the current node is in the sibling set.
Next Root. A hash of the siblings and the current node yields the next-level root.
Final Constraint. The top-level root is constrained to match the public Merkle root.

Range Check

The range check ensures a given value is less than $2^{chunk_size \times chunks}$ . It is used to cap note balances (for example, 14 chunks of 8 bits each for a max of $2^{112} - 1$ ). If a value overflows this limit, it will fail to generate a valid proof.

Gate Constraint

For a single advice column $z$ and a lookup table $T = {0, 1, \dots, 2^{chunk_size} - 1}$ , the gate enforces:

z_{i} - z_{i + 1} \times 2^{chunk_size} \in T .

Here, $a_{i} = z_{i} - z_{i + 1} \times 2^{chunk_size}$ is the value to range check.

Running Sum

To range check a value that is larger than the $2^{chunk_size}$ encoded in the lookup table, the value can be split into smaller parts, forming the running sums of fixed-size chunks. A circuit then can be synthesized to check the running sums of the value with range check for each chunk. The running sum constraints can be constructed as follows:

Chunk Decomposition
The value is split into $chunks$ pieces, each under $2^{chunk_size}$ .
Running Sum Construction

$z_{0} = value, z_{i} = 2^{chunk_size} \cdot z_{i + 1} + a_{i}, z_{chunks} = 0 .$

If $z_{chunks} \neq 0$ , the value overflowed.

Note Hash

Whenever a new note is created, its hash needs to be inserted as a leaf in the Merkle tree on-chain. To submit a Merkle proof for the new note, it needs to prove the knowledge of the note using NoteChip.

A note comprises of the fields:

[
 version,
 id,
 nullifier,
 trapdoor,
 token_balance,
 token_address
]

Before creating a note hash, it first generates a hash for the asset [token_balance, token_address], and then generates the hash using:

[
 version,
 id,
 nullifier,
 trapdoor,
 h_balance
]

The circuit also enforces a constant constraint on the version field, meaning it only supports a specific note version.

MAC Commitment

The MAC commitment is essentially a signature over the viewing key. It is used by the Anonymity Revoker (AR) to track transactions related to a given viewing key. To prove the MAC commitment is correct, the prover must supply a correct viewing key derived from the id that is already part of the note hash. The circuit checks:

Hash(r, key) matches the MAC commitment in the public inputs, where r is the salt value and the key is the viewing key.
r matches the MAC salt that is in the public inputs.

Circuits

A proof for a new note can be generated through one of the three circuit types: new_account, deposit, and withdraw.

Common to all three circuits are checks on: The nullifier, used to invalidate the old note. The note hash, which is added to the Merkle tree. The MAC commitment, which allows the AR to link transactions if necessary.

New account note

When an account is first created (e.g., during an initial deposit), it must generate a proof for the new note through circuit new_account. Different from deposit and withdraw circuits, it includes ElGamal encryption of the viewing key as an additional public input:

// public inputs
pub enum NewAccountInstance {
  HashedNote,
  Prenullifier,
  InitialDeposit,
  TokenAddress,
  AnonymityRevokerPublicKeyX,
  AnonymityRevokerPublicKeyY,
  EncryptedKeyCiphertext1X,
  EncryptedKeyCiphertext1Y,
  EncryptedKeyCiphertext2X,
  EncryptedKeyCiphertext2Y,
  MacSalt,
  MacCommitment,
}

Here, it checks the $(c_{1}, c_{2})$ EncryptedKeyCiphertext** against the AR’s public key AnonymityRevokerPublicKey*, by applying ElGamal encryption to the viewing key.

Additionally, different from the nullifier in the other two note types, the Prenullifier, which is hash(id), is to prevent an account id from being reused to create multiple new account notes.

Deposit note

A deposit note adds assets to an existing account. It requires that the prover demonstrates the knowledge of the previous note via a Merkle proof using the MerkleCircuit, and validates the updated balance in the new note.

n e w_b a l a n c e = o l d_b a l a n c e + d e p o s i t_v a l u e

To prove the knowledge of the previous note, it needs to compute the hash of the previous note and its inclusion proof in the Merkle tree with private witness path and public input MerkleRoot. In order to invalidate the previous note on the contract when adding a new note, it checks the nullifier hash of the previous note as a public input.

// private witnesses
pub struct DepositProverKnowledge<T> {
    // Old note
    pub id: T,
    pub nullifier_old: T,
    pub trapdoor_old: T,
    pub account_old_balance: T,
    pub token_address: T,

    // Merkle proof
    pub path: [[T; ARITY]; NOTE_TREE_HEIGHT],

    // New note
    pub nullifier_new: T,
    pub trapdoor_new: T,

    // Salt for MAC.
    pub mac_salt: T,
    pub deposit_value: T,
}

The public inputs reveal the new note hash HashedNewNote and one of the Merkle roots MerkleRoot for the contract to update the Merkle tree to include the new note. In addition, it also reveals HashedOldNullifier to invalidate the previous note.

// public inputs
pub enum DepositInstance {
  MerkleRoot,
  HashedOldNullifier,
  HashedNewNote,
  DepositValue,
  TokenAddress,
  MacSalt,
  MacCommitment,
}

The DepositValue and TokenAddress are for the contract to validate the actual deposited asset value.

Withdraw note

The withdrawal note is to prove the intent to withdraw some of the asset balance from an existing note. It does mostly the same checks as the deposit note, except that it also does the range check on the new balance and withdraw commitment.

For withdrawal, it needs to ensure the previous note has enough balance for the withdrawal amount. Otherwise, the balance value in the new note will be underflowed. Since the maximum values of the balance and the withdrawal amount is $2^{112} - 1$ , and the field size is around $2^{254}$ , the underflowed balance will be far more than $2^{112}$ . So it is sufficient to use the RangeCheckChip to constrain the new balance to be less than $2^{112}$ to avoid underflow.

During withdrawal on the contract, it needs to specify some additional withdrawal details for the contract to process. To prevent a front-running attack against the proof, the proof attaches a commitment as a public input, which is a hash of these withdrawal details:

// commitment to the withdrawal details
bytes memory commitment = abi.encodePacked(
 CONTRACT_VERSION,
    addressToUInt256(withdrawalAddress),
    addressToUInt256(relayerAddress),
 relayerFee,
 chainId,
 pocketMoney
);

Shielder Smart Contract

The Shielder smart contract holds all funds (including the Native token and ERC20 tokens) and maintains the state of each account. It stores the history of notes as hashes in a Merkle tree for inclusion proof and nullifier hash set to avoid double spending. Below is a typical flow during deposit action:

The user generates a Halo2 proof for the Note transition during the deposit. They call depositERC20 with the proof and other public inputs, such as oldNullifierHash, the new note hash, and mac.
The contract verifies the circuit proof, ensuring the old Note exists in the given Merkle root and that the Note transition is valid.
The contract enforces that oldNullifierHash is not in the nullifier hash set and inserts it into the set, marking the old Note as consumed.
The contract inserts the new Note hash into the note-hash Merkle tree.
The contract transfers the given amount of tokens from the sender to itself and emits a Deposit event.

The Merkle tree in Shielder has an arity of 7 and a height of 13, supporting up to $7^{13} \approx 2^{36}$ leaves. It uses the Poseidon2 hash over the BN254 scalar field. This configuration is mainly to reduce the overhead of the Halo2 circuit.

Shielder SDK

The Shielder SDK on scope consisted of mainly two parts, the Rust crates used for WASM bindings (shielder-bindings, shielder-account and type-conversions) and the Typescript client packages (Shielder-sdk, Shielder-sdk-crypto and Shielder-sdk-crypto-wasm). Those packages essentially encode the client side logic of the Shielder protocol and have the following main functions:

To handle the generation of IDs that are used for various chains and tokens
To implement the logic that maintains the local status of a client (which transactions they have made on which chain)
To generate proofs for NewAccount, Deposit and Withdraw actions and call the smart contract to commit them on chain

The SDK allows a client to have a local main account which depends on a given private key. By design, all other important intermediate secrets used in the Shielder protocol are derived from this private ID. In particular:

For every chain_id and every (consecutive, starting with zero) token index Index, an ID is generating using the private_key by hashing the concatenation of these values:

{ID}_{c h a i n, t o k e n} = H (p r i v a t e_k e y,'ID', c h a i n_i d, I n d e x)

Given an ${ID}_{c h a i n, t o k e n}$ and a nonce a nullifier is generated as:

nullifier = H ({ID}_{c h a i n, t o k e n},'Nullifier', n o n c e)

Similarly a trapdoor is generated as:

trapdoor = H ({ID}_{c h a i n, t o k e n},'Trapdoor', n o n c e)

These derivation functions are defined in crates/shielder-account/src/secrets.rs. This design thus implies the following: A client $C$ with tokens on multiple chains will have:

An ID family for a given chain (chain_id)
An ID for every token on a given chain_id, which is indexed starting from $0$ . That, is if he has 3 tokens for a given chain_id, there will be 3 IDs, one for each token, with indexes $0, 1$ and $2$ .
Every time an action is performed (new account, deposit or withdraw) the nonce is incremented to compute a new nullifier and trapdoor.

Therefore by design, for every token, there is a seemingly random ID, and for every action, a corresponding random nullifier and a trapdoor. Those also look seemingly random without known the ID (random seed), which is private to the ZKP circuits. At the same time, from a given key an account can be recovered by recomputing the necessary IDs.

State persistence and synchronization

For local persistence of an account’s state, the SDK implements an abstract interface InjectedStorageInterface that can be instantiated to interact with the browser’s localStorage or some other file system or local database. It is the implementers responsibility to make sure that persistent states are stored securely (i.e. encrypted). State transitions on-chain are monitored by the synchronization logic specified in shielder-sdk/src/state/sync/synchronizer.ts. Here, for each chain ID and token, it is checked whether a given nullifier is marked as spent, by querying the block of the nullifier through the Nullifier.sol smart-contract.

Findings

Below are listed the findings found during the engagement. High severity findings can be seen as so-called "priority 0" issues that need fixing (potentially urgently). Medium severity findings are most often serious findings that have less impact (or are harder to exploit) than high-severity findings. Low severity findings are most often exploitable in contrived scenarios, if at all, but still warrant reflection. Findings marked as informational are general comments that did not fit any of the other criteria.

ID	Component	Name	Risk
#00	protocol design	User's Account Can Be Poisoned in NewAccount and Deposit Transactions	Medium
#01	contracts/Shielder.sol	Missing Field Check for `macSalt` and `macCommitment` in the Contract	Informational
#02	Contract / New Account circuit	Contract or Circuit Should Check if Revoker’s Public Key is on the Grumpkin Curve	Informational
#03	protocol design	Unnecessary Trapdoor Value in the Note	Informational

#00 - User's Account Can Be Poisoned in NewAccount and Deposit Transactions

Severity: Medium Location: protocol design

Description. In the NewAccount and Deposit transaction, the proof does not commit to the sender of the fund. Anyone with the proof can deposit funds into the user’s account. A malicious actor can front-run a user’s transaction and deposit illicit funds into a user’s account to poison it.

In the depositERC20 function of the contract below, it transfers token from the sender to Shielder and verifies the proof of the Note transition. The proof does not enforce the sender of the fund, and anyone with the proof can perform the deposit action into the user’s account.

/*
* Makes an ERC20 token deposit into the Shielder.
*/
function depositERC20(
    bytes3 expectedContractVersion,
    address tokenAddress,
    uint256 amount,
    uint256 oldNullifierHash,
    uint256 newNote,
    uint256 merkleRoot,
    uint256 macSalt,
    uint256 macCommitment,
    bytes calldata proof
) external whenNotPaused {
    IERC20 token = IERC20(tokenAddress);
    if (
        amount > MAX_CONTRACT_BALANCE ||
        token.balanceOf(address(this)) + amount > MAX_CONTRACT_BALANCE
    ) {
        revert ContractBalanceLimitReached();
    }
    // verify the proof of Note transition
    uint256 newNoteIndex = _deposit(
        expectedContractVersion,
        tokenAddress,
        amount,
        oldNullifierHash,
        newNote,
        merkleRoot,
        macSalt,
        macCommitment,
        proof
    );

    token.safeTransferFrom(msg.sender, address(this), amount);
    [...]
}

Although the proof can only be generated by the account owner, in blockchain context the transaction will be public before it is committed on-chain. Then a malicious actor can front-run a user’s deposit transaction and deposit funds from an illicit address to the user’s account (the deposit amount must be the same as the one specified in the proof). As a result, the user’s account is poisoned by the illicit fund. The Anonymity Revoker may have to decrypt an innocent user’s account to track the illicit funds. This will undermine the privacy of the user. The malicious actor might do this for the purpose of confusing the public or revealing the user’s account.

Recommendation. It is recommended to enforce that the sender is authorized in NewAccount and Deposit transactions. This ensures only authorized addresses can deposit funds into a user’s account.

Client Response. This issue was fixed in https://github.com/Cardinal-Cryptography/zkOS-circuits/pull/90 and https://github.com/Cardinal-Cryptography/zkOS-monorepo/pull/210.

#01 - Missing Field Check for `macSalt` and `macCommitment` in the Contract

Severity: Informational Location: contracts/Shielder.sol

Description. The macSalt and macCommitment values are emitted by the circuit for the Revoker to track the transactions of an account. In the contract, they are passed as uint256 values and are not checked to be less than FIELD_MODULUS. f the range is not checked in the verifier either, a user could submit values like macSalt + FIELD_MODULUS and still pass verification. This could confuse the Revoker, though it can always normalize the values into the valid field range.

function _deposit(
    bytes3 expectedContractVersion,
    address tokenAddress,
    uint256 amount,
    uint256 oldNullifierHash,
    uint256 newNote,
    uint256 merkleRoot,
    uint256 macSalt,
    uint256 macCommitment,
    bytes calldata proof
)
    private
    restrictContractVersion(expectedContractVersion)
    fieldElement(oldNullifierHash)
    fieldElement(newNote)
    returns (uint256)
{
    [...]
    publicInputs[5] = macSalt;
    publicInputs[6] = macCommitment;
    [...]
}

Recommendation. It is recommended to explicitly enforce that macSalt and macCommitment are within the field’s valid range.

Client Response. This issue was fixed in https://github.com/Cardinal-Cryptography/zkOS-monorepo/pull/209.

#02 - Contract or Circuit Should Check if Revoker’s Public Key is on the Grumpkin Curve

Severity: Informational Location: Contract / New Account circuit

Description. The anonymity revoker’s public key is an ElGamal public key represented as a point in the Grumpkin curve. This public key is used by the New Account circuit to prove that the viewing_key has been correctly encrypted using ElGamal. In the AnonymityRevoker.sol contract a comment points out that it is important to check whether this public key is indeed on the curve (line 13):

// IMPORTANT: curve point should be validated in the circuit or the contract!

However this check is not done either on the contract nor the circuit. This is recommended to have defense in depth, in case a malicious actor manages to change the value of the public key to something off the curve, which would sabotage the anonymity revocation logic.

Recommendation. Either the contract or the New Account circuit should check whether the revoker’s key is on the curve.

Client Response. This issue was fixed in https://github.com/Cardinal-Cryptography/zkOS-monorepo/pull/211.

#03 - Unnecessary Trapdoor Value in the Note

Severity: Informational Location: protocol design

Description. trapdoor is designed to be like a “private key” to prove the ownership of the note. This is possibly redundant because (a.) the id and nullifier are already always private and (b.) the trapdoor is derived deterministically from the id. It seems the id and nullifier should be sufficient to prove the note ownership.

Although the presence of this unused trapdoor in the note won’t pose immediate security issues, it might cause confusions to the protocol for the time being and possibly introduce unnecessary complexity across the toolchain, such as in the client SDK and in the circuit.

Recommendation. Either document the need for the trapdoor or consider removing it.

Client Response. This issue was fixed in https://github.com/Cardinal-Cryptography/zkOS-circuits/pull/91 and https://github.com/Cardinal-Cryptography/zkOS-monorepo/pull/212.

← Back to Index